题目内容
已知函数y=f(x)的图象如图所示,则下列说法中错误的是( )
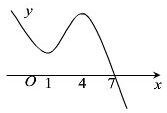

| A、f(x)在区间(-∞,1)上单调递减 |
| B、f(x)在区间(1,4)上单调递增 |
| C、当4<x<7时,f'(x)>0 |
| D、当x=1时,f'(x)=0 |
考点:函数的单调性与导数的关系
专题:函数的性质及应用,导数的综合应用
分析:通过图象显然看出A,B的说法正确;x=1是f(x)的极值点,所以f′(1)=0,所以D的说法正确;并且看出当4<x<7时,函数f(x)单调递减,所以f′(x)<0,所以C的说法错误.
解答:
解:由图象可知:f(x)在区间(-∞,1)上单调递减,在(1,4)上单调递增,x=1是f(x)的极值点,
∴f′(1)=0,
当4<x<7时,f(x)单调递减,
∴f′(x)<0;
∴说法错误的是C.
故选C.
∴f′(1)=0,
当4<x<7时,f(x)单调递减,
∴f′(x)<0;
∴说法错误的是C.
故选C.
点评:考查通过函数图象判断函数的单调性,函数极值点的概念,函数单调性和函数导数符号的关系.

练习册系列答案
相关题目
在如图所示的程序框图中输入10,结果会输出( )


| A、10 | B、11 |
| C、512 | D、1 024 |
我们已学过的算法有求解一元二次方程的求根公式,加减消元法求二元一次方程组解,二分法求函数零点等.对算法的描述有:
①对一类问题都有效;
②对个别问题有效;
③计算可以一步步地进行,每一步都有惟一的结果;
④是一种通法,只要按部就班地做,总能得到结果.
以上正确描述算法的有( )
①对一类问题都有效;
②对个别问题有效;
③计算可以一步步地进行,每一步都有惟一的结果;
④是一种通法,只要按部就班地做,总能得到结果.
以上正确描述算法的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知an=logn+1(n+2)(n∈N*),观察下列运算:
a1•a2=log23•log34=
•
=2;
a1•a2•a3•a4•a5•a6=log23•log34•…•log78=
•
•…•
=3;….
若a1•a2•a3•…•ak(k∈N*)为整数,则称k为“企盼数”,试确定当a1•a2•a3•…•ak=2 014时,“企盼数”k为( )
a1•a2=log23•log34=
| lg3 |
| lg2 |
| lg4 |
| lg3 |
a1•a2•a3•a4•a5•a6=log23•log34•…•log78=
| lg3 |
| lg2 |
| lg4 |
| lg3 |
| lg8 |
| lg7 |
若a1•a2•a3•…•ak(k∈N*)为整数,则称k为“企盼数”,试确定当a1•a2•a3•…•ak=2 014时,“企盼数”k为( )
| A、22014+2 |
| B、22014 |
| C、22014-2 |
| D、22014-4 |
已知函数f(x)=sin(
+2x)sin(
-2x),则函数f(x)的图象( )
| π |
| 4 |
| π |
| 4 |
A、关于点(
| ||
B、关于点(
| ||
C、关于直线x=-
| ||
D、关于直线x=-
|
已知a,b为两条直线,α,β为两个平面,下列命题中正确的是( )
| A、若α∥b,β∥b,则α∥β |
| B、若α∥a,α∥b,则a∥b |
| C、若a⊥α,b⊥β,则α∥β |
| D、若a⊥α,a⊥β,则α∥β |
下列命题中,满足“p∨q”为真,“p∧q”为假,“¬p”为真是( )
| A、p:0=∅,q:0∈∅ | ||||
| B、p:在△ABC中,若cos2A=cos2B,则A=B;q:y=cosx在第一象限是减函数 | ||||
C、p:a+b≥2
| ||||
D、p:函数y=
|
定义域为R的奇函数f(x)单调递增,且对任意实数a,b满足f(a)+f(b-1)=0,则a+b=( )
| A、-1 | B、0 | C、1 | D、不确定 |