题目内容
已知an=logn+1（n+2）（n∈N*），观察下列运算：
a1•a2=log23•log34=
•
=2；
a1•a2•a3•a4•a5•a6=log23•log34•…•log78=
•
•…•
=3；…．
若a1•a2•a3•…•ak（k∈N*）为整数，则称k为“企盼数”，试确定当a1•a2•a3•…•ak=2 014时，“企盼数”k为（ ）
a1•a2=log23•log34=
| lg3 |
| lg2 |
| lg4 |
| lg3 |
a1•a2•a3•a4•a5•a6=log23•log34•…•log78=
| lg3 |
| lg2 |
| lg4 |
| lg3 |
| lg8 |
| lg7 |
若a1•a2•a3•…•ak（k∈N*）为整数，则称k为“企盼数”，试确定当a1•a2•a3•…•ak=2 014时，“企盼数”k为（ ）
| A、22014+2 |
| B、22014 |
| C、22014-2 |
| D、22014-4 |
考点：数列与函数的综合
专题：等差数列与等比数列
分析：由已知得lg（k+2）=lg 22014，由此能求出k．
解答：
解：由已知得a1•a2•a3•…•ak=
=2 014，
lg（k+2）=lg 22014，
解得k=22014-2．
故选：C．
| lg(k+2) |
| lg2 |
lg（k+2）=lg 22014，
解得k=22014-2．
故选：C．
点评：本题考查“企盼数”k的求法，是中档题，解题时要注意对数性质的合理运用．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
相关题目
在复平面内，复数（2+i）2对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
|
| A、充要 |
| B、必要不充分 |
| C、充分不必要 |
| D、既不充分也不必要 |
在等差数列{an}中，a1+3a8+a15=120，则2a6-a4的值为（ ）
| A、24 | B、22 | C、20 | D、-8 |
已知函数y=f（x）的图象如图所示，则下列说法中错误的是（ ）
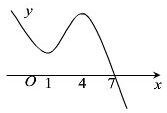
| A、f（x）在区间（-∞，1）上单调递减 |
| B、f（x）在区间（1，4）上单调递增 |
| C、当4＜x＜7时，f'（x）＞0 |
| D、当x=1时，f'（x）=0 |
已知函数y=f（x）是R上的奇函数，且当x≥0时f（x）=x2-2x，则f（x）在（-∞，0]上的解析式是（ ）
| A、f（x）=x2-2x |
| B、f（x）=-x2-2x |
| C、f（x）=-x2+2x |
| D、f（x）=x2+2x |
函数y=
的导数是（ ）
| 1 |
| x |
| A、y'=ex | ||
| B、y'=lnx | ||
C、y′=
| ||
| D、y'=-x-2 |