题目内容
双曲线C：
（φ为参数）的一个焦点为（ ）
|
| A、（3，0） |
| B、（4，0） |
| C、（5，0） |
| D、（0，5） |
考点：参数方程化成普通方程
专题：坐标系和参数方程
分析：sec2φ-tan2φ=1．即可得出
-
=1，再利用双曲线的性质即可得出．
| x2 |
| 9 |
| y2 |
| 16 |
解答：
解：双曲线C：
（φ为参数），
∵sec2φ-tan2φ=1．
∴
-
=1，
∴c=
=5．
∴此双曲线的一个焦点为（5，0）．
故选：C．
|
∵sec2φ-tan2φ=1．
∴
| x2 |
| 9 |
| y2 |
| 16 |
∴c=
| 9+16 |
∴此双曲线的一个焦点为（5，0）．
故选：C．
点评：本题考查了同角三角函数基本关系式、双曲线的性质，属于基础题．
练习册系列答案
相关题目
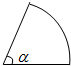现要用篱笆围成一个面积为S扇形菜园（如图所示），问要使这个菜园所用篱笆最短，则这个扇形的半径和圆心角各为（ ）A、
| ||
B、2
| ||
C、
| ||
D、2
|
函数f（x）=2sin（ωx+φ）（ω＞0，已知i为虚数单位，则 （1-i）2的值等于（ ）
| A、2-2i | B、2+2i |
| C、-2i | D、2i |
已知点M（2，-3），N（-3，-2），直线ax+y-1-a=0与线段MN相交，则实数a的取值范围是（ ）
A、-
| ||
B、-4≤a≤
| ||
C、a≤-
| ||
D、a≤-4或a≥
|
已知向量
与
的夹角为θ，|
|=2，|
|=1，
=t
，
=（1-t）
，|
|在t0时取得最小值．当0＜t0＜
时，夹角θ的取值范围为（ ）
| OA |
| OB |
| OA |
| OB |
| OP |
| OA |
| OQ |
| OB |
| PQ |
| 1 |
| 5 |
A、（0，
| ||||
B、（
| ||||
C、（
| ||||
D、（0，
|
已知|
|=4，
是单位向量，向量
与
的夹角是
，则|
+
|=（ ）
| a |
| e |
| a |
| e |
| 3π |
| 4 |
| a |
| 2 |
| e |
A、2
| ||
B、4+
| ||
C、
| ||
D、
|
已知函数f（x）=lg
，若f（a）=b（b≠0），则f（-a）等于（ ）
| 1-x |
| 1+x |
| A、-b | ||
| B、b | ||
C、
| ||
D、-
|