已知函数f（x）满足f（x）•f（-x）=1，f（x）＞0恒成立，则函数g（x）=
的奇偶性（ ）
| f(x)-1 |
| f(x)+1 |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |
已知定义域为R的函数f （x）满足对任意的x1，x2∈（8，+∞）（x1＜x2），有f（x1）＞f（x2），且函数y=f（x+8）为偶函数，则（ ）
| A、f （6）＞f （7） |
| B、f （6）＞f （9） |
| C、f （7）＞f （9） |
| D、f （7）＞f （10） |
已知函数f（n）=
，则f（3）的值是（ ）
|
| A、6 | B、24 | C、120 | D、720 |
如图，在△ABC中，
=2
，记
=
，
=
，则
=（ ）
| CD |
| DB |
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
证明命题：“f（x）=ex+
在（0，+∞）上是增函数”，现给出的证法如下：
因为f（x）=ex+
，所以f′（x）=ex-
，
因为x＞0，所以ex＞1，0＜
＜1，
所以ex-
＞0，即f′（x）＞0，
所以f（x）在（0，+∞）上是增函数，使用的证明方法是（ ）
| 1 |
| ex |
因为f（x）=ex+
| 1 |
| ex |
| 1 |
| ex |
因为x＞0，所以ex＞1，0＜
| 1 |
| ex |
所以ex-
| 1 |
| ex |
所以f（x）在（0，+∞）上是增函数，使用的证明方法是（ ）
| A、综合法 | B、分析法 |
| C、反证法 | D、以上都不是 |
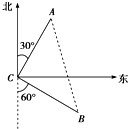两灯塔A、B与海洋观察站C的距离都等于2| 2 |
| A、2 km |
| B、3 km |
| C、4 km |
| D、5 km |
O为坐标原点，F为抛物线C：y2=4x的焦点，P为C上一点，若|PF|=4，则△POF的面积为（ ）
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
直线y=1-x交抛物线y2=2px（p＞0）于M，N两点，且|
+
|=|
-
|，则p的值为（ ）
| OM |
| ON |
| OM |
| ON |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|