题目内容
设函数,f(x)=|x-a|
(Ⅰ)当a=2,解不等式,f(x)≥5-|x-1|;
(Ⅱ)若f(x)≤1的解集为[0,2],
+
=a(m>0,n>0),求证:m+2n≥4.
(Ⅰ)当a=2,解不等式,f(x)≥5-|x-1|;
(Ⅱ)若f(x)≤1的解集为[0,2],
| 1 |
| m |
| 1 |
| 2n |
考点:绝对值不等式的解法,基本不等式
专题:不等式的解法及应用
分析:(Ⅰ)当a=2,不等式即|x-2|+|x-1|≥5.由绝对值的意义可得-1和4到1、2的距离之和正好等于5,从而求得|x-2|+|x-1|≥5的解集.
(Ⅱ)由f(x)≤1求得 a-1≤x≤a+1,再根据f(x)≤1的解集为[0,2],可得a=1,再根据 m+2n=(m+2n)(
+
)=2+
+
,利用基本不等式证得要证的不等式.
(Ⅱ)由f(x)≤1求得 a-1≤x≤a+1,再根据f(x)≤1的解集为[0,2],可得a=1,再根据 m+2n=(m+2n)(
| 1 |
| m |
| 1 |
| 2n |
| 2n |
| m |
| m |
| 2n |
解答:
解:(Ⅰ)当a=2,不等式f(x)≥5-|x-1|,即|x-2|+|x-1|≥5.
由绝对值的意义可得,|x-2|+|x-1|表示数轴上的x对应点到1、2的距离之和,而-1和4到1、2的距离之和正好等于5,
故|x-2|+|x-1|≥5的解集为(-∞,-1]∪[4,+∞).
(Ⅱ)由f(x)≤1 可得-1≤x-a≤1,求得 a-1≤x≤a+1,
再根据f(x)≤1的解集为[0,2],可得a=1.
故有
+
=1(m>0,n>0),∴m+2n=(m+2n)(
+
)=2+
+
≥4,
当且仅当
=
时,等号成立,故m+2n≥4成立.
由绝对值的意义可得,|x-2|+|x-1|表示数轴上的x对应点到1、2的距离之和,而-1和4到1、2的距离之和正好等于5,
故|x-2|+|x-1|≥5的解集为(-∞,-1]∪[4,+∞).
(Ⅱ)由f(x)≤1 可得-1≤x-a≤1,求得 a-1≤x≤a+1,
再根据f(x)≤1的解集为[0,2],可得a=1.
故有
| 1 |
| m |
| 1 |
| 2n |
| 1 |
| m |
| 1 |
| 2n |
| 2n |
| m |
| m |
| 2n |
当且仅当
| 2n |
| m |
| m |
| 2n |
点评:本题主要考查绝对值的意义,绝对值不等式的解法,基本不等式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程ln(x+1)-
=0,(x>0)的根存在的大致区间是( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(3,4) |
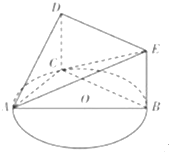 如图,已知三角形ABC内接于圆O,AB为圆O的直径,四边形DCBE为平行四边形,CD⊥平面ABC,AB=2,tan∠EAB=
如图,已知三角形ABC内接于圆O,AB为圆O的直径,四边形DCBE为平行四边形,CD⊥平面ABC,AB=2,tan∠EAB=