题目内容
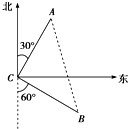两灯塔A、B与海洋观察站C的距离都等于2| 2 |
| A、2 km |
| B、3 km |
| C、4 km |
| D、5 km |
考点：解三角形的实际应用
专题：计算题,解三角形
分析：由两个方位角的度数得出∠ACB=90°，又知AC=BC=2
km，△ACB为等腰直角三角形，利用勾股定理可得边AB的长度．
| 2 |
解答：
解：由图知：∠ACB=90°，
在Rt△ACB中，AB2=AC2+BC2=（2
）2+（2
）2=16，
∴AB=4km，
故选C．
在Rt△ACB中，AB2=AC2+BC2=（2
| 2 |
| 2 |
∴AB=4km，
故选C．
点评：本题考查解三角形的实际应用，关键是如何把实际问题转化为数学问题，然后套用题目提供的对应关系解决问题．
练习册系列答案
相关题目
设椭圆C：
+
=1（a＞b＞0）的左、右焦点分别为F1，F2，P是C上的点，PF2⊥F1F2，∠PF1F2=60°，则C的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2-
|
已知函数f（x）满足f（x）•f（-x）=1，f（x）＞0恒成立，则函数g（x）=
的奇偶性（ ）
| f(x)-1 |
| f(x)+1 |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |
已知函数f（x）=x|x-2|