题目内容
O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=4,则△POF的面积为( )
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据抛物线方程求得抛物线的准线方程与焦点坐标,利用|PF|=4,求得P点的横坐标,代入抛物线方程求得纵坐标,代入三角形面积公式计算.
解答:
解:由抛物线方程得:抛物线的准线方程为:x=-1,焦点F(1,0),
又P为C上一点,|PF|=4,∴xP=3,
代入抛物线方程得:|yP|=2
,
∴S△POF=
×|0F|×|yP|=
.
故选:B.
又P为C上一点,|PF|=4,∴xP=3,
代入抛物线方程得:|yP|=2
| 3 |
∴S△POF=
| 1 |
| 2 |
| 3 |
故选:B.
点评:本题考查了抛物线的定义及几何性质,熟练掌握抛物线上的点所迷住的条件是解题的关键.

练习册系列答案
相关题目
数列{an}中,a2=2,a6=0且数列{
}是等差数列,则a8=( )
| 1 |
| an+1 |
A、
| ||
B、
| ||
C、-
| ||
D、
|
抛物线y=2ax2(a≠0)焦点坐标是( )
A、(
| ||
B、(0,
| ||
C、(
| ||
D、(0,
|
已知定义域为R的函数f (x)满足对任意的x1,x2∈(8,+∞)(x1<x2),有f(x1)>f(x2),且函数y=f(x+8)为偶函数,则( )
| A、f (6)>f (7) |
| B、f (6)>f (9) |
| C、f (7)>f (9) |
| D、f (7)>f (10) |
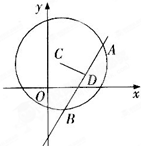 已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.