题目内容
已知函数f(x)满足f(x)•f(-x)=1,f(x)>0恒成立,则函数g(x)=
的奇偶性( )
| f(x)-1 |
| f(x)+1 |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |
考点:函数奇偶性的判断
专题:
分析:利用奇偶函数的定义,判断g(-x)与g(x)的关系.
解答:
解:由已知,f(x)•f(-x)=1,f(x)>0,∴f(-x)=
,
∴g(-x)=
=
=
=-g(x),
∴g(x)为奇函数;
故选A.
| 1 |
| f(x) |
∴g(-x)=
| f(-x)-1 |
| f(-x)+1 |
| ||
|
| 1-f(x) |
| 1+f(x) |
∴g(x)为奇函数;
故选A.
点评:本题考查了函数的奇偶性的判断;在定义域关于原点对称的情况下,判断f(-x)与f(x)的关系.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
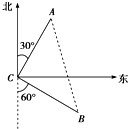 两灯塔A、B与海洋观察站C的距离都等于2
两灯塔A、B与海洋观察站C的距离都等于2| 2 |
| A、2 km |
| B、3 km |
| C、4 km |
| D、5 km |
若变量x,y满足约束条件
则Z=2x-y的最大值为( )
|
| A、2 | B、5 | C、1 | D、4 |