定义域为[a,b]的函数y=f(x)的图象的两个端点A、B,M(x,y)是f(x)图象上任意一点,其中x=λa+(1-λ)b(λ∈R),向量
=λ
+(1-λ)
,其中O为坐标原点,若不等式|
|≤k恒成立,则称函数f(x)在[a,b]上“k阶线性近似”.若函数y=x+
在[1,2]上“k阶线性近似”,则实数k的取值范围为( )
| ON |
| OA |
| OB |
| MN |
| 1 |
| x |
| A、[0,+∞) | ||||
| B、[1,+∞) | ||||
C、[
| ||||
D、[
|
现定义一种变换:对于一个由有限个数组成的序列S0,将其中的每个数换成该数在S0中出现的次数,可得到一个新序列S1,例如序列S0:(4,2,3,4,2),通过变换可生成新序列S1:(2,2,1,2,2),若S0可以为任意序列,则下面的序列可作为S1的是( )
| A、(1,2,1,2,2) |
| B、(2,2,2,3,3) |
| C、(1,1,2,2,3) |
| D、(1,2,1,1,2) |
在直三棱柱ABC-A1B1C1中,AA1=2,二面角B-AA1-C1的大小等于60°,B到面AC1的距离等于
,C1到面AB1的距离等于2
,则直线BC1与直线AB1所成角的正切值等于( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
若函数f(x)(x∈R)是奇函数,则( )
| A、函数f (x2)是奇函数 |
| B、函数[f (x)]2是奇函数 |
| C、函数f (x)•x2是奇函数 |
| D、函数f(x)+x2是奇函数 |
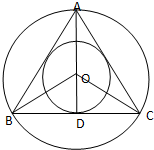 如图,在正三角形ABC中,
如图,在正三角形ABC中,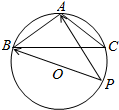 如图,在△ABC中,三内角A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,a=
如图,在△ABC中,三内角A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,a=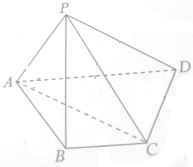 如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.
如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.