题目内容
若函数f（x）（x∈R）是奇函数，则（ ）
| A、函数f （x2）是奇函数 |
| B、函数[f （x）]2是奇函数 |
| C、函数f （x）•x2是奇函数 |
| D、函数f（x）+x2是奇函数 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：根据函数奇偶性的定义进行判断即可．
解答：
解：若函数f（x）（x∈R）是奇函数，则
A．f（（-x）2）=f（x2），则函数f（x2）是偶函数，故A错误，
B．[f（-x）]2=[-f（x）]2，则函数[f（x）]2是偶函数，故B错误，
C．函数f（-x）•（-x）2=-f（x）•x2，则函数f（x）•x2是奇函数，故C正确，
D．f（-x）+（-x）2=-f（x）+x2≠f（x）+x2，且f（-x）+（-x）2≠-f（x）-x2，则函数f（x）+x2是奇函数错误，故D错误，
故选：C．
A．f（（-x）2）=f（x2），则函数f（x2）是偶函数，故A错误，
B．[f（-x）]2=[-f（x）]2，则函数[f（x）]2是偶函数，故B错误，
C．函数f（-x）•（-x）2=-f（x）•x2，则函数f（x）•x2是奇函数，故C正确，
D．f（-x）+（-x）2=-f（x）+x2≠f（x）+x2，且f（-x）+（-x）2≠-f（x）-x2，则函数f（x）+x2是奇函数错误，故D错误，
故选：C．
点评：本题主要考查函数奇偶性的判断，根据函数奇偶性的定义是解决本题的关键．
练习册系列答案
相关题目
已知全集U=R，A={x|x≤0}，B={x|x＞-1}，则集合∁U（A∩B）=（ ）
| A、{x|-1＜x≤0} |
| B、{x|-1≤x≤0} |
| C、{x|x≤-1或x≥0} |
| D、{x|x≤-1或x＞0} |
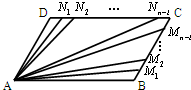已知平行四边形ABCD，点M1，M2，M3，…，Mn-1和N1，N2，N3，…，Nn-1分别将线段BC和DC，n等分（n∈N*，n≥2），如图，若| AM1 |
| AM2 |
| AMn-1 |
| AN1 |
| AN2 |
| ANn-1 |
| AC |
| A、29 | B、30 | C、31 | D、32 |
由“a＞b，则a+c＞b+c”推理到“a＞b，则ac＞bc”是（ ）
| A、归纳推理 | B、类比推理 |
| C、演绎推理 | D、都不是 |