Question

在平面三角形中，若ABC的三边长为a，b，c，其内切圆半径为r，有结论：ABC的面积S=

1

2

（a+b+c）r，类比该结论，则在空间四面体ABCD中，若四个面的面积分别为S₁，S₂，S₃，S₄，其内切球半径为R，则有相应结论：

 

．

Answer 1

考点：类比推理

专题：推理和证明

分析：先用面积分割法，证明平面内的结论正确．然后将该命题推广到空间：若四面体四个面的面积分别为S₁，S₂，S₃，S₄，内切球的半径为R，则此四面体的体积为：V=

1

3

（S₁+S₂+S₃+S₄）R．接下来可以用体积分割的方法，类似地证明推广到空间的结论也是正确的．

解答： 解：先证明平面内的结论正确．
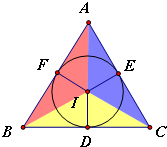设△ABC的内切圆圆心为I，圆I与BC、CA、AB分别相切于点D、E、F，
连接ID、IE、IF，
∵ID与圆I相切于点D，
∴ID⊥BC，可得三角形IBC的面积为S_△IBC=

1

2

BC•ID=

1

2

ar（其中r是△ABC的内切圆半径），
同理可得：S_△IAC=

1

2

AC•IE=

1

2

br，S_△IAB=

1

2

AB•IF=

1

2

cr，
∴三角形ABC的面积为S=S_△IBC+S_△IAC+S_△IAB=

1

2

ar+

1

2

br+

1

2

cr=

1

2

（a+b+c）r，
根据此结论，将其类比到空间可得：
若四面体四个面的面积分别为S₁，S₂，S₃，S₄，内切球的半径为R，则此四面体的体积为V=

1

3

（S₁+S₂+S₃+S₄）R．
证明如下：

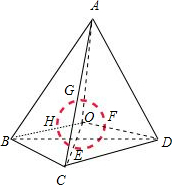
设四面体ABCD的内切球为球O，球O分别切面BCD、面ACD、面ABD、面ABC于E、F、G、H，
分别设S_△BCD、S_△ACD、S_△ABD、S_△ABC为S₁、S₂、S₃、S₄
∵球O切平面BCD于点E，
∴OE⊥平面BCD，三棱锥O-BCD的体积为V₁=

1

3

S_△BCD•OE=

1

3

S₁R，
同理可得：三棱锥O-BCD的体积为V₂=

1

3

S_△ACD•OF=

1

3

S₂R，三棱锥O-ABD的体积为V₃=

1

3

S_△ABD•OG=

1

3

S₃R，
三棱锥O-ABC的体积为V₄=

1

3

S_△ABC•OH=

1

3

S₄R，
∴四面体ABCD的体积等于V=V₁+V₂+V₃+V₄=

1

3

S₁R+

1

3

S₂R+

1

3

S₃R+

1

3

S₄R=

1

3

（S₁+S₂+S₃+S₄）R．
故答案为：V=

1

3

（S₁+S₂+S₃+S₄）R．

点评：本题借助于一个平面内关于内切圆半径的正确命题，通过将其推广到空间的一个结论，考查了三角形面积公式和锥体体积公式等知识点，以及用割补的方法求几何体体积的思想，属于中档题．