题目内容
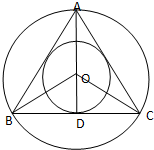 如图,在正三角形ABC中,
如图,在正三角形ABC中,| 内切圆半径 |
| 外接圆半径 |
| OD |
| OA |
| OD |
| AD-OD |
| ||
1-
|
| OD |
| AD |
| S△OBC |
| S△ABC |
| 1 |
| 3 |
| 内切圆半径 |
| 外接圆半径 |
| 1 |
| 2 |
| 内切球的半径r |
| 外接球的半径R |
考点:类比推理
专题:推理和证明
分析:本题考查的知识点是类比推理,在由平面几何的性质类比推理空间立体几何性质时,我们常用的思路是:由平面几何中点的性质,类比推理空间几何中线的性质;由平面几何中线的性质,类比推理空间几何中面的性质;由平面几何中面的性质,类比推理空间几何中体的性质;或是将一个二维平面关系,类比推理为一个三维的立体关系,故类比平面内三角形的性质,我们可以推断四面体的相关性质.
解答:
解:在由平面几何的性质类比推理空间立体几何性质时,我们常用的思路是:
由平面几何中点的性质,类比推理空间几何中线的性质;
由平面几何中线的性质,类比推理空间几何中面的性质;
由平面几何中面的性质,类比推理空间几何中体的性质;
或是将一个二维平面关系,类比推理为一个三维的立体关系,
故类比在正三角形ABC中,
=
=
=
,而
=
=
,所以
=
.
可得:在正四面体ABCD(每个面都是正三角形的四面体)中,
=
=
=
,而
=
=
,
所以
=
,
故答案为:
由平面几何中点的性质,类比推理空间几何中线的性质;
由平面几何中线的性质,类比推理空间几何中面的性质;
由平面几何中面的性质,类比推理空间几何中体的性质;
或是将一个二维平面关系,类比推理为一个三维的立体关系,
故类比在正三角形ABC中,
| 内切圆半径 |
| 外接圆半径 |
| OD |
| OA |
| OD |
| AD-OD |
| ||
1-
|
| OD |
| AD |
| S△OBC |
| S△ABC |
| 1 |
| 3 |
| 内切圆半径 |
| 外接圆半径 |
| 1 |
| 2 |
可得:在正四面体ABCD(每个面都是正三角形的四面体)中,
| 内切球的半径r |
| 外接球的半径R |
| OE |
| OA |
| OE |
| AE-OE |
| ||
1-
|
| OE |
| OA |
| VO-BCD |
| VA-BCD |
| 1 |
| 4 |
所以
| 内切球的半径r |
| 外接球的半径R |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).但类比推理的结论不一定正确,还需要经过证明,我们在进行类比推理时,一定要注意对结论进行进一步的论证,如果要证明一个结论是正确的,要经过严密的论证,但要证明一个结论是错误的,只需要举出一个反例.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
设M={平面内的点(a,b)},N={f(x)|f(x)=acos2x+bsin2x},给出M到N的映射f:(a,b)→f(x)=acos2x+bsin2x,则点(1,
)的象f(x)的最小正周期为( )
| 3 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
已知复数z=1-i(其中i为虚数单位),则
等于( )
| 2i |
| z |
| A、1-i | B、1+i |
| C、-1-i | D、-1+i |
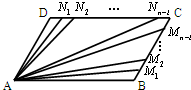 已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DC,n等分(n∈N*,n≥2),如图,若
已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DC,n等分(n∈N*,n≥2),如图,若| AM1 |
| AM2 |
| AMn-1 |
| AN1 |
| AN2 |
| ANn-1 |
| AC |
| A、29 | B、30 | C、31 | D、32 |
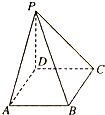 如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PD⊥底面ABCD,且PD=a,PA=PC=
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PD⊥底面ABCD,且PD=a,PA=PC=| 2 |
(1)求证:点A在PA为直径的圆上;
(2)若在这个四棱锥内放一球,求此球的最大半径.
已知正四面体ABCD的棱长为1,则
•
=(( )
| AB |
| CD |
A、-
| ||
B、
| ||
| C、1 | ||
| D、0 |
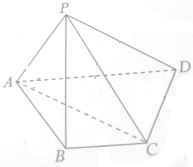 如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.
如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.