题目内容
在直三棱柱ABC-A1B1C1中,AA1=2,二面角B-AA1-C1的大小等于60°,B到面AC1的距离等于
,C1到面AB1的距离等于2
,则直线BC1与直线AB1所成角的正切值等于( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
考点:异面直线及其所成的角
专题:计算题,空间位置关系与距离,空间角
分析:运用线面垂直的性质结合二面角的定义可得二面角B-AA1-C1的平面角即为∠BAC,且为60°,由面面垂直的性质定理可得B到AC的距离为
,C到AB的距离为2
,即可得到BC=2
,AB=2,∠ABC=90°,再由向量
BC1与AB1的数量积及夹角公式求出余弦值,由同角的平方关系和商数关系,即可计算得到正切值.
| 3 |
| 3 |
| 3 |
BC1与AB1的数量积及夹角公式求出余弦值,由同角的平方关系和商数关系,即可计算得到正切值.
解答:
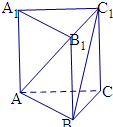 解:直三棱柱ABC-A1B1C1中,AA1⊥底面ABC,则AA1⊥AB,AA1⊥AC,
解:直三棱柱ABC-A1B1C1中,AA1⊥底面ABC,则AA1⊥AB,AA1⊥AC,
则二面角B-AA1-C1的平面角即为∠BAC,且为60°,
B到面AC1的距离等于
,由于侧面和底面垂直,
由面面垂直的性质定理可得,即为B到AC的距离为
,
同样C1到面AB1的距离等于2
,即为C到AB的距离为2
,
在三角形ABC中,可得BC=2
,AB=2,∠ABC=90°,
则
•
=(
-
)•(
+
)=
2+
•
-
•
-
•
=4+0-0-0=4,
|
|=
=2
,|
|=
=4,
则cos<
,
>=
=
=
.
则sin<
,
>=
=
,
即有tan<
,
>=
=
.
故选:A.
 解:直三棱柱ABC-A1B1C1中,AA1⊥底面ABC,则AA1⊥AB,AA1⊥AC,
解:直三棱柱ABC-A1B1C1中,AA1⊥底面ABC,则AA1⊥AB,AA1⊥AC,则二面角B-AA1-C1的平面角即为∠BAC,且为60°,
B到面AC1的距离等于
| 3 |
由面面垂直的性质定理可得,即为B到AC的距离为
| 3 |
同样C1到面AB1的距离等于2
| 3 |
| 3 |
在三角形ABC中,可得BC=2
| 3 |
则
| AB1 |
| BC1 |
| BB1 |
| BA |
| BB1 |
| BC |
| BB1 |
| BB1 |
| BC |
| BA |
| BB1 |
| BA |
| BC |
=4+0-0-0=4,
|
| AB1 |
| 4+4 |
| 2 |
| BC1 |
| 4+12 |
则cos<
| AB1 |
| BC1 |
| ||||
|
|
| 4 | ||
2
|
| ||
| 4 |
则sin<
| AB1 |
| BC1 |
1-
|
| ||
| 4 |
即有tan<
| AB1 |
| BC1 |
| ||||
|
| 7 |
故选:A.
点评:本题考查异面直线所成角的求法:向量法,考查二面角的平面角的定义,考查空间直线和平面的位置关系,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知集合A={x|x≤-2或x≥1},B={x|0≤x≤1},则( )
| A、A∩B=∅ |
| B、(∁RA)⊆B |
| C、-1∈A∪B |
| D、1∈A∩B |
设F为双曲线
-
=1(a>0,b>0)的右焦点,P是双曲线上的点,若它的渐近线上存在一点Q(在第一象限内),使得
=2
,则双曲线离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| FP |
| PQ |
| A、(1,3) |
| B、(3,+∞) |
| C、(1,2) |
| D、(2,+∞) |
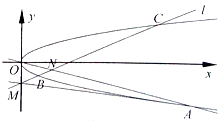 在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为 x=-
在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为 x=-