已知函数y=cos x（x∈[-
，
]）的图象与x轴围成的区域记为M，若随机在圆O：x2+y2=π2内任取一点，则该点在区域M内的概率是（ ）
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
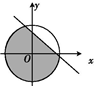区域D是平面直角坐标系中由到原点距离不大于1的点组成，在区域D内任取一点（x，y），该点满足x+y＜
| ||
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知直线a，平面α、β，且a?α．①α⊥β；②a⊥β；③a∥α，以这三个条件中的两个为题设，余下一个为结论组成命题，其中真命题有（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
已知m，n是两条不重合的直线，α，β，γ是三个两两不重合的平面，给出下列四个命题
①若m⊥α，m⊥β，则α∥β；
②若α⊥β，β⊥γ，则α∥β；
③若m?a，n?β，m∥n，则α∥β；
④若m，n是异面直线，n?α，m∥β，n?β，n∥α，则α∥β．
其中真命题是（ ）
①若m⊥α，m⊥β，则α∥β；
②若α⊥β，β⊥γ，则α∥β；
③若m?a，n?β，m∥n，则α∥β；
④若m，n是异面直线，n?α，m∥β，n?β，n∥α，则α∥β．
其中真命题是（ ）
| A、①和② | B、①和③ |
| C、①和④ | D、③和④ |
设直线过点（0，a），其斜率为
，且与圆（x-2）2+y2=4相切，则正数a的值为（ ）
| 3 |
| 4 |
| A、1 | B、2 | C、3 | D、4 |
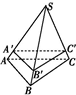已知正棱锥S-ABC的底面边长为4，高为3，在正棱锥内任取一点P，使得VP-ABC＜| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|