题目内容
已知函数y=cos x(x∈[-
,
])的图象与x轴围成的区域记为M,若随机在圆O:x2+y2=π2内任取一点,则该点在区域M内的概率是( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:利用定积分求出区域M的面积,再由几何概型的概率公式解答.
解答:
解:区域M的面积为
cos xdx=2
cos xdx=2sin x
=2,
所以点在区域M内的概率是P=
=
.
故选:D
| ∫ |
-
|
| ∫ |
0 |
|
所以点在区域M内的概率是P=
| 2 |
| π×π2 |
| 2 |
| π3 |
故选:D
点评:本题考查了利用定积分求曲边梯形的面积以及几何概型的概率公式的运用,属于基础题目,经常考查.

练习册系列答案
相关题目
已知数列{an}的前n项和为Sn,满足Sn=4an-p,其中p为非零常数.
(1)求证:数列{an}成等比数列;
(2)若a2=
,数列{bn}满足bn+1=bn+an,b1=2,求{bn}的通项公式.
(1)求证:数列{an}成等比数列;
(2)若a2=
| 4 |
| 3 |
对于平面α,β,γ和直线a,b,m,n,下列命题中真命题是( )
| A、若α∥β,α∩γ=a,β∩γ=b,则a∥b |
| B、若a∥b,b⊆α,则a∥α |
| C、若a⊆β,b⊆β,a∥α,b∥α,则β∥α |
| D、若a⊥m,a⊥n,m⊆α,n⊆α,则a⊥α |
执行如图所示的程序框图,则该程序运行后输出的k的值是( )


| A、3 | B、4 | C、5 | D、6 |
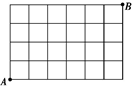 某市新城区有7条南北向街道,5条东西向街道(如图).
某市新城区有7条南北向街道,5条东西向街道(如图).