题目内容
已知直线a,平面α、β,且a?α.①α⊥β;②a⊥β;③a∥α,以这三个条件中的两个为题设,余下一个为结论组成命题,其中真命题有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:分别判断①②⇒③,①③⇒②,②③⇒①是否正确.
解答:
解:由题意可得:②a⊥α①α⊥β又a?α⇒③a∥β,由空间中线面的位置关系可得此结论正确.所以①②⇒③正确.
③a∥α①α⊥β⇒②a⊥α不正确,还有可能是a∥α.所以①③⇒②错误.
③a∥α②a⊥β⇒①α⊥β,根据面面垂直的定义可得此结论是正确的.所以③②⇒①正确.
故选C.
③a∥α①α⊥β⇒②a⊥α不正确,还有可能是a∥α.所以①③⇒②错误.
③a∥α②a⊥β⇒①α⊥β,根据面面垂直的定义可得此结论是正确的.所以③②⇒①正确.
故选C.
点评:解决此类问题的关键是熟练掌握空间中有关线面的位置关系,利用有关的判断定理与性质定理解决问题.

练习册系列答案
相关题目
已知函数f(x)=
,满足对任意x1≠x2,都有
<0成立,则实数a的取值范围是( )
|
| f(x1)-f(x2) |
| x1-x2 |
| A、(0,1] | ||
B、(0,
| ||
| C、(0,3] | ||
D、(0,
|
下列各图中,可表示函数y=f(x)的图象的只可能是( )
A、 |
B、 |
C、 |
D、 |
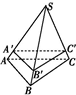 已知正棱锥S-ABC的底面边长为4,高为3,在正棱锥内任取一点P,使得VP-ABC<
已知正棱锥S-ABC的底面边长为4,高为3,在正棱锥内任取一点P,使得VP-ABC<| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|