题目内容
9.已知向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$是共面的三个向量,其中$\overrightarrow{a}$=($\sqrt{2}$,2),|$\overrightarrow{b}$|=2$\sqrt{3}$,|$\overrightarrow{c}$|=2$\sqrt{6}$,$\overrightarrow{a}$∥$\overrightarrow{c}$.(Ⅰ)求|$\overrightarrow{c}$-$\overrightarrow{a}$|;
(Ⅱ)若$\overrightarrow{a}$-$\overrightarrow{b}$与3$\overrightarrow{a}$+2$\overrightarrow{b}$垂直,求$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$)的值.
分析 (Ⅰ)根据$\overrightarrow{a}$∥$\overrightarrow{c}$,$\overrightarrow{c}$、$\overrightarrow{a}$共线,求出|$\overrightarrow{c}$-$\overrightarrow{a}$|的模长即可;
(Ⅱ)根据$\overrightarrow{a}$-$\overrightarrow{b}$与3$\overrightarrow{a}$+2$\overrightarrow{b}$垂直数量积为0,求出$\overrightarrow{a}$•$\overrightarrow{b}$的值,再讨论$\overrightarrow{a}$、$\overrightarrow{c}$共线同向和反向时,求出$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$)的值.
解答 解:(Ⅰ)∵$\overrightarrow{a}$=($\sqrt{2}$,2),|
∴|$\overrightarrow{a}$|=$\sqrt{6}$,
又|$\overrightarrow{c}$|=2$\sqrt{6}$,且$\overrightarrow{a}$∥$\overrightarrow{c}$,
∴|$\overrightarrow{c}$-$\overrightarrow{a}$|=|$\overrightarrow{c}$|+|$\overrightarrow{a}$|=2$\sqrt{6}$+$\sqrt{6}$=3$\sqrt{6}$,
或|$\overrightarrow{c}$-$\overrightarrow{a}$|=|$\overrightarrow{c}$|-|$\overrightarrow{a}$|=2$\sqrt{6}$-$\sqrt{6}$=$\sqrt{6}$;
(Ⅱ)∵$\overrightarrow{a}$-$\overrightarrow{b}$与3$\overrightarrow{a}$+2$\overrightarrow{b}$垂直,
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•(3$\overrightarrow{a}$+2$\overrightarrow{b}$)=0,
∴3${\overrightarrow{a}}^{2}$-2${\overrightarrow{b}}^{2}$-$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即3×${(\sqrt{6})}^{2}$-2×${(2\sqrt{3})}^{2}$-$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=-6,
当$\overrightarrow{a}$、$\overrightarrow{c}$共线同向时,$\overrightarrow{a}$•$\overrightarrow{c}$=$\sqrt{6}$×2$\sqrt{6}$=12,
∴$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$)=${\overrightarrow{a}}^{2}$+$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{a}$•$\overrightarrow{c}$=${(\sqrt{6})}^{2}$-6+12=12;
当$\overrightarrow{a}$、$\overrightarrow{c}$共线反向时,$\overrightarrow{a}$•$\overrightarrow{c}$=-$\sqrt{6}$×2$\sqrt{6}$=-12,
$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$)=${\overrightarrow{a}}^{2}$+$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{a}$•$\overrightarrow{c}$=${(\sqrt{6})}^{2}$-6-12=-12.
点评 本题考查了平面向量的数量积与模长公式的应用问题,也考查了共线定理的应用问题,是综合性题目.

| A. | 若$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,且$\overrightarrow{a}$与$\overrightarrow{b}$同向,则$\overrightarrow{a}$>$\overrightarrow{b}$ | B. | 当实数λ=0时,λ$\overrightarrow{a}$=0 | ||
| C. | |$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | D. | |$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
| A. | $\frac{8}{3}$ | B. | $\frac{11}{3}$ | C. | 4 | D. | 8 |
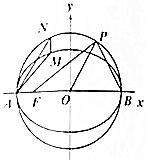 已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.
已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点. 已知四棱锥P-ABCD的直观图与三视图如图所示,其中正(主)视图与侧(左)视图为直角三角形,俯视图为正方形(数据如图所示),已知该几何体的体积为$\frac{2}{3}$.
已知四棱锥P-ABCD的直观图与三视图如图所示,其中正(主)视图与侧(左)视图为直角三角形,俯视图为正方形(数据如图所示),已知该几何体的体积为$\frac{2}{3}$.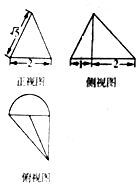 某几何体的三视图如图所示,则该几何体的体积是$\frac{π}{3}$+$\frac{4}{3}$.
某几何体的三视图如图所示,则该几何体的体积是$\frac{π}{3}$+$\frac{4}{3}$.