题目内容
4. 已知四棱锥P-ABCD的直观图与三视图如图所示,其中正(主)视图与侧(左)视图为直角三角形,俯视图为正方形(数据如图所示),已知该几何体的体积为$\frac{2}{3}$.
已知四棱锥P-ABCD的直观图与三视图如图所示,其中正(主)视图与侧(左)视图为直角三角形,俯视图为正方形(数据如图所示),已知该几何体的体积为$\frac{2}{3}$.(1)求实数a的值;
(2)将△PAB绕PB旋转一周,求所得旋转体的体积.
分析 (1)利用棱锥的体积公式,可得结论;
(2)求出PB,利用棱锥的体积公式,可得结论.
解答 解:(1)由题意$\frac{1}{3}×1×1×a$=$\frac{2}{3}$,∴a=2;
(2)由题意,PB=$\sqrt{1+4}$=$\sqrt{5}$,AB⊥平面PBC,
可得AB⊥PB,
∴旋转体的体积V=$\frac{1}{3}π•5•1$=$\frac{5π}{3}$.
点评 本题考查三视图,考查棱锥的体积公式,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
12.P为△ABC边BC上的点,满足3$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,则$\frac{1}{m}$+$\frac{2}{n}$的最小值为( )
| A. | $\frac{2\sqrt{2}}{3}$+1 | B. | 2$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$+3 |
19.若动点A(x1,y1)、B(x2,y2)分别在直线l1:2x-y+11=0和l2:2x-y-1=0上移动,则AB的中点M所在的直线方程为( )
| A. | 2x+y-5=0 | B. | 2x+y+5=0 | C. | 2x-y-5=0 | D. | 2x-y+5=0 |
14.为了得到函数y=1-2sin2(x-$\frac{π}{12}$)的图象,可以将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{3}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
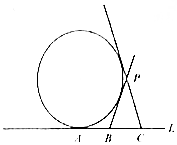 如图,A,B,C是直线l上的三点,AB=4,BC=4,过A作动圆与直线l相切,过B,C分别做圆的异于l的两切线,交于点P,则P的轨迹为椭圆.(填轨迹类型,不求方程)
如图,A,B,C是直线l上的三点,AB=4,BC=4,过A作动圆与直线l相切,过B,C分别做圆的异于l的两切线,交于点P,则P的轨迹为椭圆.(填轨迹类型,不求方程)