题目内容
20.已知双曲线C的渐近线方程为y=±$\frac{1}{2}$x,点(3,$\sqrt{2}$)在双曲线上.(1)求双曲线C的方程;
(2)过点P(0,1)的直线l交双曲线C于A,B两点,交x轴于点Q(点Q与双曲线的顶点不重合),当$\overrightarrow{PQ}$=λ$\overrightarrow{QA}$=μ$\overrightarrow{QB}$,且λ•μ=-5时,求直线l的方程.
分析 (1)设双曲线的方程为:x2-4y2=m(≠0),把点(3,$\sqrt{2}$)代入双曲线方程即可得出.
(2)由题意可得:直线l的斜率存在且不为0,则可设l的方程为:y=kx+1,A(x1,y1),B(x2,y2),可得Q$(-\frac{1}{k},0)$.
由$\overrightarrow{PQ}$=λ$\overrightarrow{QA}$,可得:A点坐标,代入在双曲线上,整理可得:(1-k2)λ2+2λ+1-4k2=0,同理可得:(1-k2)μ2+2μ+1-4k2=0,可把λ,μ看作二次方程:(1-k2)x2+2x+1-4k2=0的两个实数根,利用λ•μ=$\frac{1-4{k}^{2}}{1-{k}^{2}}$=-5时,解得k即可得出.
解答 解:(1)设双曲线的方程为:x2-4y2=m(≠0),把点(3,$\sqrt{2}$)代入双曲线方程可得:x2-4y2=1.
(2)由题意可得:直线l的斜率存在且不为0,则可设l的方程为:y=kx+1,A(x1,y1),B(x2,y2),可得Q$(-\frac{1}{k},0)$.
由$\overrightarrow{PQ}$=λ$\overrightarrow{QA}$,可得:$\left\{\begin{array}{l}{{x}_{1}=-\frac{1}{k}-\frac{1}{λk}}\\{{y}_{1}=-\frac{1}{λ}}\end{array}\right.$,∵A在双曲线上,∴$(-\frac{1}{k}-\frac{1}{λk})^{2}$-4$(-\frac{1}{λ})^{2}$=1,整理可得:(1-k2)λ2+2λ+1-4k2=0,同理可得:(1-k2)μ2+2μ+1-4k2=0,
若1-k2=0,则直线l经过顶点,舍去,∴1-k2≠0.
可把λ,μ看作二次方程:(1-k2)x2+2x+1-4k2=0的两个实数根,
∴λ•μ=$\frac{1-4{k}^{2}}{1-{k}^{2}}$=-5时,解得k2=$\frac{2}{3}$.
此时△>0,∴k=±$\frac{\sqrt{6}}{3}$,则直线方程为:y═±$\frac{\sqrt{6}}{3}$x+1.
点评 本题考查了双曲线的标准方程及其性质、直线与双曲线相交问题、向量运算性质、一元二次方程的根与系数的关系、不等式的解法,考查了推理能力与计算能力,属于难题.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案| A. | $\frac{2\sqrt{2}}{3}$+1 | B. | 2$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$+3 |
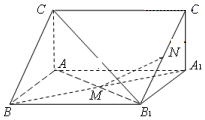 如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点
如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点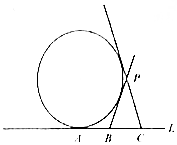 如图,A,B,C是直线l上的三点,AB=4,BC=4,过A作动圆与直线l相切,过B,C分别做圆的异于l的两切线,交于点P,则P的轨迹为椭圆.(填轨迹类型,不求方程)
如图,A,B,C是直线l上的三点,AB=4,BC=4,过A作动圆与直线l相切,过B,C分别做圆的异于l的两切线,交于点P,则P的轨迹为椭圆.(填轨迹类型,不求方程)