如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3，那么c的值等于（ ）
A. 8
B. 14
C. 8或14
D. -8或-14
C
【解析】根据题意，得
，
解得c=8或14．
故选：C． 抛物线
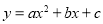与x轴的两个交点为（﹣1，0），（3，0），其形状与抛物线
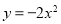相同，则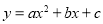的函数关系式为（ ）
A．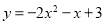
B．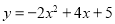
C．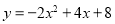
D．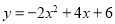
D．
【解析】
试题分析：由题意a=﹣2，∵抛物线与x轴的两个交点为（﹣1，0），（3，0）∴设y=﹣2（x+1）（x﹣3），即：．故选D． 若所求的二次函数图象与抛物线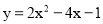
有相同的顶点，并且在对称轴的左侧，y随x的增大而增大，在对称轴的右侧，y随x的增大而减小，则所求二次函数的解析式为（ ）
A.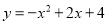 
B.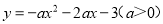 
C.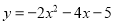 
D.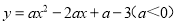 
D
【解析】抛物线y=2x2-4x-1的顶点坐标为（1，-3），根据题意得所求的二次函数的解析式的顶点坐标是（1，-3），且抛物线开口向下．
A．抛物线开口向下，顶点坐标是（1，5），所以选项错误；
B．抛物线开口向下，顶点坐标是（1，-3a-3），所以选项错误；
C．抛物线开口向下，顶点坐标是（-1，-3），所以选项错误；
D．抛物线开口向下，顶点坐标是（1，-3）... 若二次函数y=ax2+bx+c的x与y的部分对应值如下表，则当x=1时，y的值为（ ）
x | -7 | -6 | -5 | -4 | -3 | -2 |
y | -27 | -13 | -3 | 3 | 5 | 3 |
A. -27
B. -13
C. -3
D. 5
A
【解析】设二次函数的解析式为，
∵当x=-4或-2时，y=3，由抛物线的对称性可知h=-3，k=5，
∴，
把（-2，3）代入得，a=-2，
∴二次函数的解析式为，
当x=1时，y=-27．
故选：A． 将二次函数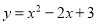
化为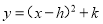
的形式，结果为（ ）
A.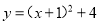 
B.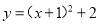 
C.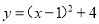 
D.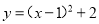 
D
【解析】
故选：D． 若二次函数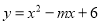
配方后为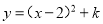
，则m，k的值分别为（ ）
A. 0，6
B. 0，2
C. 4，6
D. 4，2
D
【解析】∵，
，
∴，
∴-4=-m，4+k=6，
∴m=4，k=2．
故选：D． 二次函数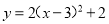
的二次项系数、一次项系数、常数项分别为（ ）
A. 2，12，20
B. 2x2，-12，20
C. 2，-12，20
D. 2，-12x，20
C
【解析】∵，
∴二次项系数为2，一次项系数为-12，常数项为20．
故选：C． 一个二次函数的图象经过点A（0，0），B（-1，-11），C（1，9）三点，则这个二次函数的关系式是（ ）
A.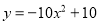 
B.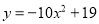 
C.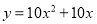 
D.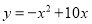 
D
【解析】由于抛物线经过原点，则可以设其函数关系式为，
将B、C两点坐标代入，得
解得
则函数关系式为
故选：D． 形状与抛物线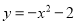
相同，对称轴是x=-2，且过点（0，3）的抛物线是（ ）
A.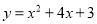 
B.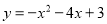 
C.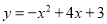 
D.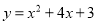 
或
D
【解析】设所求抛物线的函数关系式为，由抛物线过点（0，3），可得：c=3，
由抛物线形状与相同，
分为两种情况：①开口向下，则a＜0，
又∵对称轴x=-2，则x==-2．则b＜0，
由此可得出B选项符合题意．
②开口向下，则a＞0，
又∵对称轴x=-2，则x==-2．则b＞0，
由此可得出A选项符合题意，
综合上述，符合条件的是选项D．
... 抛物线与x轴交点的横坐标为-2和1，且过点（2，8），它的关系式为（ ）
A.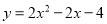 
B.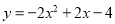 
C.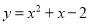 
D.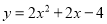 
D
【解析】由题意，设抛物线解析式为，将（2，8）代入，可得
，
解得a=2，
∴抛物线的解析式为： ，
化简，得．
故选：D．