题目内容
将二次函数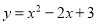
化为
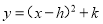的形式，结果为（ ）
A.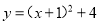 
B.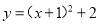 
C.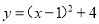 
D.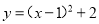 
D
【解析】
故选：D．
练习册系列答案
小学教材全测系列答案
相关题目
下列由左到右的变形中，哪些是分解因式?哪些不是?请说出理由.
（1）a（x+y）=ax+ay；
（2）x2+2xy+y2-1＝x（x+2y）+（y +1）（y-1）；
（3）ax2-9a＝a（x+3）（x-3）；
（4）x2+2+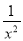
=
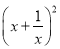
（5）2a3＝2a·a·a.
见解析
【解析】试题分析：根据因式分解的定义判断即可.
试题解析：
因为(1) (2)的右边都不是整式的积的形式.所以它们不是分解因式；(4)中， 都不是整式，(5)中的2a3不是多项式，所以它们也不是分解因式．只有(3)的左边是多项式，右边是整式的积的形式，所以(3)是分解因式. 如图，已知二次函数y=ax2+bx+c的图象过A(2，0)，B(0，-1)和C(4，5)三点．
(1)求二次函数的解析式；
(2)设二次函数的图象与x轴的另一个交点为D，求点D的坐标；
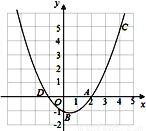
(3)在同一坐标系中画出直线y=x+1，并写出当x在什么范围内时，一次函数的值大于二次函数的值．
（1）y=x2-x-1； （2）（-1，0）；（3）见图象
【解析】（1）根据二次函数y=ax2+bx+c的图象过A（2，0），B（0，-1）和C（4，5）三点，代入得出关于a，b，c的三元一次方程组，求得a，b，c，从而得出二次函数的解析式；
（2）令y=0，解一元二次方程，求得x的值，从而得出与x轴的另一个交点坐标；
（3）画出图象，再根据图象直接得出答案．
【解析】
（1）... 把抛物线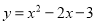
化为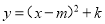
的形式，其中m，k为常数，则m-k=_________
5
【解析】，
∴m=1，k=-4，
∴m-k=1+4=5，
故答案为：5． 抛物线与x轴交点的横坐标为-2和1，且过点（2，8），它的关系式为（ ）
A.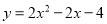 
B.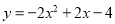 
C.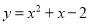 
D.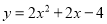 
D
【解析】由题意，设抛物线解析式为，将（2，8）代入，可得
，
解得a=2，
∴抛物线的解析式为： ，
化简，得．
故选：D． 与
形状相同的抛物线解析式为（ ）
A. y=
B. 
C. 
D. 
D
【解析】抛物线的形状只与a有关，a相等，形状就相同，∴中，a=2．
故选：D． 若小李做m个零件需用1小时，则他做1个零件需__________小时，做30个零件需_________小时．
【解析】小李做m个零件需用1小时，则他做1个零件需小时，做30个零件需小时，
故答案为： ， . ―抛物线与x轴的交点是A(－2，0)，B(1，0)，且经过点C(2，8)．
(1)求该抛物线的解析式；
(2)求该抛物线的顶点坐标．
(1) y＝2x2＋2x－4(2)(－，－ )
【解析】分析:（1）因为已知抛物线与x轴两交点坐标，则设交点式y=a(x+2)(x-1，然后把c(2,8代入求出a即可；（2）把（1）中的函数解析式转化为顶点式，可以直接得到答案.
本题解析：
(1)设这个抛物线的解析式为y=ax2＋bx＋c．将A(－2，0)，B(1，0)，C(2，8)三点代入，得解这个方程组，得∴所求抛物线的解析... ( 本小题满分10分)如图，已知：在平行四边形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．求证：
⑴△AEH≌△CGF；
⑵四边形EFGH是菱形．
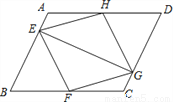
（1）证明见试题解析；（2）证明见试题解析．
【解析】试题分析：(1)、由全等三角形的判定定理SAS证得结论；(2)、易证四边形EFGH是平行四边形，那么EF∥GH，那么∠HGE=∠FEG，而EG是角平分线，易得∠HEG=∠FEG，根据等量代换可得∠HEG=∠HGE，从而有HE=HG，易证四边形EFGH是菱形．
试题解析：（1）、如图，∵四边形ABCD是平行四边形， ∴∠A=∠C，
...