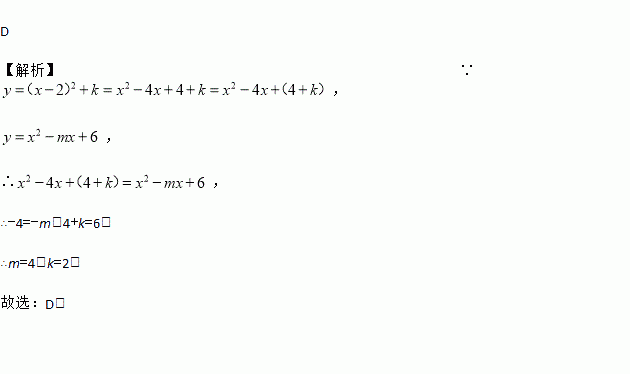题目内容
若二次函数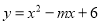
配方后为
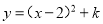，则m，k的值分别为（ ）
A. 0，6
B. 0，2
C. 4，6
D. 4，2
D
【解析】∵，
，
∴，
∴-4=-m，4+k=6，
∴m=4，k=2．
故选：D．
若关于x的多项式3x2+mx+n分解因式的结果为(3x+2)(x-1)，求m、n的值.
m=-1,n=-2.
【解析】试题分析：把(3x+2)(x-1)利用多项式乘以多项式的法则展开，与多项式3x2+mx+n比较，即可得m、n的值.
试题解析：
由题意可得：(3x+2)(x-1)=3x2+2x-3x-2=3x2-x-2=3x2+mx+n，
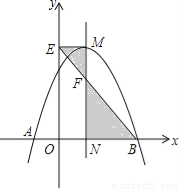
所以m=-1,n=-2. 如图，抛物线
与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F.已知点A的坐标为（﹣1，0）.
（1）求该抛物线的解析式及顶点M的坐标；
（2）求△EMF与△BNF的面积之比.
（1），（1，4）；（2）.
【解析】试题分析：（1）直接将（﹣1，0）代入求出即可，再利用配方法求出顶点坐标.
（2）利用EM∥BN，则△EMF∽△BNF，进而求出△EMF与△BNE的面积之比．
试题解析：【解析】
（1）∵点A在抛物线上，
∴，解得：c=3，
∴抛物线的解析式为.
∵，
∴抛物线的顶点M（1，4）；
（2）∵A（﹣1，0），抛物... 用一根长为80cm的铁丝，把它弯成一个矩形，设矩形的面积为ycm2，一边长为xcm，则y与x的函数表达式为___________（化为一般式）
【解析】由题意得：矩形的另一边长=80÷2-x=40-x，
∴y=x（40-x）=．
故答案为：． 将二次函数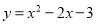
化成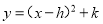
形式，则h+k结果为（ ）
A. -5
B. 5
C. -3
D. 3
C
【解析】．
则h=1，k=-4，
∴h+k=-3．
故选：C． 如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3，那么c的值等于（ ）
A. 8
B. 14
C. 8或14
D. -8或-14
C
【解析】根据题意，得
，
解得c=8或14．
故选：C． 一项工作，若甲单独完成需x小时，则甲每小时完成工作的________.若甲、乙合作 需8小时完成，则乙每小时完成工作的_______.
【解析】一项工作，若甲单独完成需x小时，则甲每小时完成工作的，
若甲、乙合作需8小时完成，则乙每小时完成工作的，
故答案为： ， . 如图所示，矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上，边OC在y轴正半轴上)绕点B逆时针旋转得到的．点O′在x轴的正半轴上，点B的坐标为(1，3)．
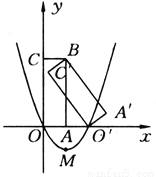
(1)如果二次函数y＝ax2+bx+c（a≠0)的图象经过O，O′两点，且图象顶点M的纵坐标为－l，求这个二次函数的解析式；
(2)在(1)中求出的二次函数图象对称轴的右侧，是否存在点P，使得△POM为直角三角形?若存在，求出点P的坐标和△POM的面积；若不存在，请说明理由；
(3)求边C′O′所在直线的解析式．
(1) y＝x2－2x(2)1(3)y=
【解析】分析:(1)连接BO,B则B0=B,求出M点坐标,列出方程组求出未知数的值,进而求出二次函数的解析式;(2)设存在满足题设条件的点P(x,y),连接OM,PM,OP,过P作PN⊥x轴,求出P点坐标和△POM的面积.(3)已知 (2,0),点D的横坐标为1,由相似关系求其纵坐标,用待定系数法求解析式.
本题解析：(1)如图2－83所示，连... 如图，□ABCD中，E是BC边的中点，连接AE，F为CD边上一点，且满足∠DFA=2∠BAE．
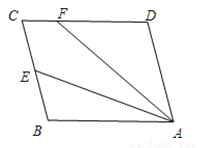
（1）若∠D=105°，∠DAF=35°．求∠FAE的度数；
（2）求证：AF=CD+CF．
（1）20°；（2）见解析
【解析】试题分析：（1）根据平行四边形的性质、平行线的性质证得；然后结合已知条件求得从而求得的度数；
（2）在AF上截取连接利用全等三角形的判定定理SAS证得 ≌，由全等三角形的对应角相等、对应边相等；然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得 最后根据线段间的和差关系证得结论．
试题解析：
（三角形内角和定理）．
∵四边...