题目内容
抛物线与x轴交点的横坐标为-2和1,且过点(2,8),它的关系式为( )
A. 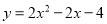
B. 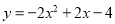
C. 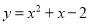
D. 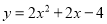
 D
【解析】由题意,设抛物线解析式为,将(2,8)代入,可得
,
解得a=2,
∴抛物线的解析式为: ,
化简,得.
故选:D.
D
【解析】由题意,设抛物线解析式为,将(2,8)代入,可得
,
解得a=2,
∴抛物线的解析式为: ,
化简,得.
故选:D.
练习册系列答案
相关题目
分解因式: 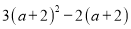 =______________.
=______________.
 (a+2)(3a+4)
【解析】提取公因式a+2即可,即原式=(a+2)(3a+6-2)=(a+2)(3a+4).
(a+2)(3a+4)
【解析】提取公因式a+2即可,即原式=(a+2)(3a+6-2)=(a+2)(3a+4). 在下列二次函数中,其图象对称轴为x=-2的是( )
A. 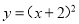
B. 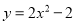
C. 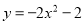
D. 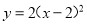
 A
【解析】根据二次函数的性质求出各个函数的对称轴,可得:
的对称轴为x=-2,故A正确;
的对称轴为x=0,故B错误;
的对称轴为x=0,故C错误;
的对称轴为x=2,故D错误.
故选:A.
A
【解析】根据二次函数的性质求出各个函数的对称轴,可得:
的对称轴为x=-2,故A正确;
的对称轴为x=0,故B错误;
的对称轴为x=0,故C错误;
的对称轴为x=2,故D错误.
故选:A. 已知二次函数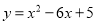 .
.
(1)解析式化为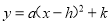 的形式;
的形式;
(2)求出该函数图象与x轴、y轴的交点坐标.
 (1)(2)(1,0),(5,0)|(0,5)
【解析】分析:(1)通过配方得到;(2)先把抛物线的解析式写成交点式得到=(x-1)(x-5),即可得到抛物线与x轴的交点坐标;把x=0代入原函数关系式可确定抛物线与y轴的交点坐标.
本题解析:(1);
(2)∵=(x-1)(x-5),
∴抛物线与x轴交点坐标为(1,0),(5,0);
令x=0,y=-5,
故抛物...
(1)(2)(1,0),(5,0)|(0,5)
【解析】分析:(1)通过配方得到;(2)先把抛物线的解析式写成交点式得到=(x-1)(x-5),即可得到抛物线与x轴的交点坐标;把x=0代入原函数关系式可确定抛物线与y轴的交点坐标.
本题解析:(1);
(2)∵=(x-1)(x-5),
∴抛物线与x轴交点坐标为(1,0),(5,0);
令x=0,y=-5,
故抛物... 如图,已知抛物线y=﹣x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),那么它对应的函数解析式是 .
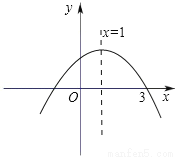
 y=﹣x2+2x+3
【解析】
试题分析:∵抛物线y=﹣x2+bx+c的对称轴为直线x=1,
∴=1,解得b=2,
∵与x轴的一个交点为(3,0),
∴0=﹣9+6+c,
解得c=3,
故函数解析式为y=﹣x2+2x+3.
故答案为:y=﹣x2+2x+3
y=﹣x2+2x+3
【解析】
试题分析:∵抛物线y=﹣x2+bx+c的对称轴为直线x=1,
∴=1,解得b=2,
∵与x轴的一个交点为(3,0),
∴0=﹣9+6+c,
解得c=3,
故函数解析式为y=﹣x2+2x+3.
故答案为:y=﹣x2+2x+3 将二次函数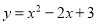 化为
化为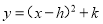 的形式,结果为( )
的形式,结果为( )
A. 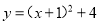
B. 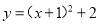
C. 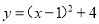
D. 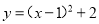
 D
【解析】
故选:D.
D
【解析】
故选:D. 某厂原计划在规定时间内生产通讯设备60台,由于改进了操作技术,每天生产的 台数比原计划多50%,结果提前两天完成任务.求改进操作技术后每天生产通讯设备多少台.
 15台.
【解析】试题分析:设改进操作技术前每天生产通讯设备x台,则改进操作技术后每天生产通讯设备1.5x台,根据提前两天完成任务,列方程求解即可.
试题解析:设改进技术前每天生产x台,根据题意,得,解得x=10,
经检验x=10是原方程的解,
则1.5x=15,
所以改进操作技术后每天生产通讯设备15台.
15台.
【解析】试题分析:设改进操作技术前每天生产通讯设备x台,则改进操作技术后每天生产通讯设备1.5x台,根据提前两天完成任务,列方程求解即可.
试题解析:设改进技术前每天生产x台,根据题意,得,解得x=10,
经检验x=10是原方程的解,
则1.5x=15,
所以改进操作技术后每天生产通讯设备15台. 下列关于x的方程中,不是分式方程的是( )
A. 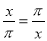 B.
B. 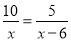 C.
C. 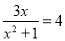 D.
D. 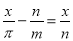
 D
【解析】A、分母中含有未知数,是分式方程,故本选项不符合题意;
B、分母中含有未知数,是分式方程,故本选项不符合题意;
C、分母中含有未知数,是分式方程,故本选项不符合题意;
D、分母中不含有未知数,不是分式方程,故本选项符合题意,
故选D.
D
【解析】A、分母中含有未知数,是分式方程,故本选项不符合题意;
B、分母中含有未知数,是分式方程,故本选项不符合题意;
C、分母中含有未知数,是分式方程,故本选项不符合题意;
D、分母中不含有未知数,不是分式方程,故本选项符合题意,
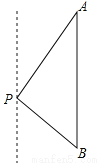
故选D. 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A. 40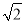 海里 B. 40
海里 B. 40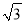 海里 C. 80海里 D. 40
海里 C. 80海里 D. 40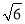 海里
海里
 A
【解析】试题分析:过点P作PD⊥AB于点D,根据方位角可得:∠A=30°,∠B=45°,根据AP=80海里可得PD=40海里,PB=40海里,故选A.
A
【解析】试题分析:过点P作PD⊥AB于点D,根据方位角可得:∠A=30°,∠B=45°,根据AP=80海里可得PD=40海里,PB=40海里,故选A. 
