��Ŀ����
��״�������� ��ͬ���Գ�����x=-2���ҹ��㣨0��3�����������ǣ� ��
��ͬ���Գ�����x=-2���ҹ��㣨0��3�����������ǣ� ��
A. 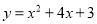
B. 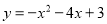
C. 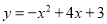
D. 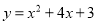 ��
��
 D
�������������������ߵĺ�����ϵʽΪ���������߹��㣨0��3�����ɵã�c=3��
����������״����ͬ��
��Ϊ����������ٿ������£���a��0��
�֡߶Գ���x=-2����x==-2����b��0��
�ɴ˿ɵó�Bѡ��������⣮
�ڿ������£���a��0��
�֡߶Գ���x=-2����x==-2����b��0��
�ɴ˿ɵó�Aѡ��������⣬
�ۺ�������������������ѡ��D��
...
D
�������������������ߵĺ�����ϵʽΪ���������߹��㣨0��3�����ɵã�c=3��
����������״����ͬ��
��Ϊ����������ٿ������£���a��0��
�֡߶Գ���x=-2����x==-2����b��0��
�ɴ˿ɵó�Bѡ��������⣮
�ڿ������£���a��0��
�֡߶Գ���x=-2����x==-2����b��0��
�ɴ˿ɵó�Aѡ��������⣬
�ۺ�������������������ѡ��D��
...
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
����ʽ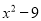 ��
��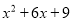 �Ĺ���ʽ��
�Ĺ���ʽ��
 x��3
���������ֱ���ʽax2-4a�����ʽx2-4x+4������ʽ�ֽ⣬��Ѱ�����ǵĹ���ʽ��
��������
��x2-9=��x-3��(x+3)��
x2+6x+9=��x+3��2��
�����ʽx2-9�����ʽx2+6x+9�Ĺ���ʽ��x+3��
x��3
���������ֱ���ʽax2-4a�����ʽx2-4x+4������ʽ�ֽ⣬��Ѱ�����ǵĹ���ʽ��
��������
��x2-9=��x-3��(x+3)��
x2+6x+9=��x+3��2��
�����ʽx2-9�����ʽx2+6x+9�Ĺ���ʽ��x+3�� ����y=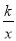 ��y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
��y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ�������
A. 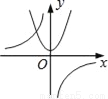 B.
B. 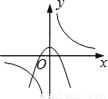 C.
C. 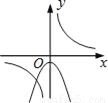 D.
D. 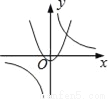
 B
��������Aѡ���У���������������ͼ������ô������Ӧ��y�ύ�ڸ����ᣬ����A�����ܣ�
Bѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����B���ܣ�
Cѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����C�����ܣ�
Dѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����D�����ܣ�
��ѡB.
...
B
��������Aѡ���У���������������ͼ������ô������Ӧ��y�ύ�ڸ����ᣬ����A�����ܣ�
Bѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����B���ܣ�
Cѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����C�����ܣ�
Dѡ���У���������������ͼ�����������߿���Ӧ�����£�����y�ύ�������ᣬ����D�����ܣ�
��ѡB.
... ��֪���κ�����ͼ���㣨0��-1������1��-3������-1��3������������κ����Ľ���ʽ��
 ������������������κ����Ľ���ʽΪ���ٰѣ�0��-1������1��-3������-1��3���ֱ����õ�����a��b��c�ķ����飬�ⷽ�������a��b��c��ֵ���Ӷ��õ����κ����Ľ���ʽ��
�������������κ����Ľ���ʽΪ��
������ã�
��ã�
�ʶ��κ����Ľ���ʽΪ��
������������������κ����Ľ���ʽΪ���ٰѣ�0��-1������1��-3������-1��3���ֱ����õ�����a��b��c�ķ����飬�ⷽ�������a��b��c��ֵ���Ӷ��õ����κ����Ľ���ʽ��
�������������κ����Ľ���ʽΪ��
������ã�
��ã�
�ʶ��κ����Ľ���ʽΪ�� ����������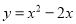 ������˵����ȷ���ǣ� ��
������˵����ȷ���ǣ� ��
A. ����������ԭ��
B. �Գ�����ֱ��x=2
C. ����ߵ�
D. ��������ԭ��
 D
���������ߣ�
��
��
�ඥ�������ǣ���1��-1�����Գ�����ֱ��x=1��
��a=1��0��������ϣ�
����Сֵ��
�ߵ�x=0ʱ�� ��
��ͼ������ԭ�㣬
��ѡ��D��
D
���������ߣ�
��
��
�ඥ�������ǣ���1��-1�����Գ�����ֱ��x=1��
��a=1��0��������ϣ�
����Сֵ��
�ߵ�x=0ʱ�� ��
��ͼ������ԭ�㣬
��ѡ��D�� �����κ���y=ax2+bx+c��x��y�IJ��ֶ�Ӧֵ���±�����x=1ʱ��y��ֵΪ��������
x | -7 | -6 | -5 | -4 | -3 | -2 |
y | -27 | -13 | -3 | 3 | 5 | 3 |
A. -27
B. -13
C. -3
D. 5
 A
������������κ����Ľ���ʽΪ��
�ߵ�x=-4��-2ʱ��y=3���������ߵĶԳ��Կ�֪h=-3��k=5��
�࣬
�ѣ�-2��3������ã�a=-2��
����κ����Ľ���ʽΪ��
��x=1ʱ��y=-27��
��ѡ��A��
A
������������κ����Ľ���ʽΪ��
�ߵ�x=-4��-2ʱ��y=3���������ߵĶԳ��Կ�֪h=-3��k=5��
�࣬
�ѣ�-2��3������ã�a=-2��
����κ����Ľ���ʽΪ��
��x=1ʱ��y=-27��
��ѡ��A�� �����з�ʽ���̣�
(1) 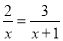 �� (2)
�� (2) 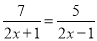 ��
��
(3) 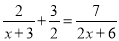 �� (4)
�� (4) 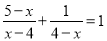 ��
��
 (1) x=2��(2) x=3��(3) x��-2�� (4)�⣮
�����������������ÿ������ȷ�����ĸ�������߳����ĸ���ѷ�ʽ����ת��Ϊ��ʽ���������ٽ��м��鼴�ɵ�.
�����������1����������ͬ��x(x+1)����
2��x+1��=3x��
��ã�x=2��
���飺��x=2ʱ��x(x+1)��0��
����ԭ���̵Ľ�Ϊx=2��
��2����������ͬ�ˣ�2x-1...
(1) x=2��(2) x=3��(3) x��-2�� (4)�⣮
�����������������ÿ������ȷ�����ĸ�������߳����ĸ���ѷ�ʽ����ת��Ϊ��ʽ���������ٽ��м��鼴�ɵ�.
�����������1����������ͬ��x(x+1)����
2��x+1��=3x��
��ã�x=2��
���飺��x=2ʱ��x(x+1)��0��
����ԭ���̵Ľ�Ϊx=2��
��2����������ͬ�ˣ�2x-1... ����ʽ����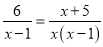 ����������������( )
����������������( )
A. x=1 B. x=1��x=0 C. x=0 D. ��ȷ��
 A
����������������ͬ��x(x-1)����
6x=x+5��
��ã�x=1��
���飺��x=1ʱ��x(x-1)=0������x=1��ԭ���̵�������ԭ�����⣬
��ѡA.
A
����������������ͬ��x(x-1)����
6x=x+5��
��ã�x=1��
���飺��x=1ʱ��x(x-1)=0������x=1��ԭ���̵�������ԭ�����⣬
��ѡA. ��ͼ����һ��ֱ�ĺ�����l����A��B�����۲�վ��AB=2km����A��ô�C�ڱ�ƫ��45��ķ���B��ô�C�ڱ�ƫ��22.5��ķ�����C�뺣����l�ľ��루��CD�ij���Ϊ��������
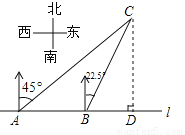
A. 4km B. ��2+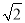 ��km C. 2
��km C. 2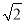 km D. ��4-
km D. ��4-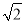 ��km
��km
 B
��������������������������з�λ�ǵ��ص㣬����B��BE��AC����AC�ڵ�E���ɡ�CAB=45�㣬AB=2km����֪BE=km�����������֪��BCA=��BCD=22.5�㣬���CB�ǡ�ACD�Ľ�ƽ���ߣ����ݽ�ƽ���ߵ����ʿɵã�BD=BE=km�����CD=AD=AB+BD=(2+)km����ѡB��
B
��������������������������з�λ�ǵ��ص㣬����B��BE��AC����AC�ڵ�E���ɡ�CAB=45�㣬AB=2km����֪BE=km�����������֪��BCA=��BCD=22.5�㣬���CB�ǡ�ACD�Ľ�ƽ���ߣ����ݽ�ƽ���ߵ����ʿɵã�BD=BE=km�����CD=AD=AB+BD=(2+)km����ѡB�� 
