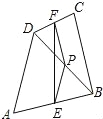
如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是 度.
 18.
【解析】
试题分析:根据中位线定理和已知,易证明△EPF是等腰三角形.∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,∴FP,PE分别是△CDB与△DAB的中位线,∴PF=BC,PE=AD,∵AD=BC,∴PF=PE,故△EPF是等腰三角形.∵∠PEF=18°,∴∠PEF=∠PFE=18°.故答案为:18.
18.
【解析】
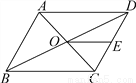
试题分析:根据中位线定理和已知,易证明△EPF是等腰三角形.∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,∴FP,PE分别是△CDB与△DAB的中位线,∴PF=BC,PE=AD,∵AD=BC,∴PF=PE,故△EPF是等腰三角形.∵∠PEF=18°,∴∠PEF=∠PFE=18°.故答案为:18. 如图,?ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
 △DOE的周长为15.
【解析】试题分析:根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=BC,所以易求△DOE的周长.
试题解析:∵平行四边形ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=O...
△DOE的周长为15.
【解析】试题分析:根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=BC,所以易求△DOE的周长.
试题解析:∵平行四边形ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
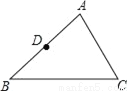
∴OD=O... 如图,已知△ABC中,D为AB的中点.
(1)请用尺规作图法作边AC的中点E,并连接DE(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若DE=4,求BC的长.
 (1)作图见解析;(2)BC=8.
【解析】试题分析:(1)作线段的垂直平分线即可.
(2)根据三角形中位线定理即可解决.
试题解析:(1)作线段的垂直平分线交于,点就是所求的点.
(2)分别为的中点,
(1)作图见解析;(2)BC=8.
【解析】试题分析:(1)作线段的垂直平分线即可.
(2)根据三角形中位线定理即可解决.
试题解析:(1)作线段的垂直平分线交于,点就是所求的点.
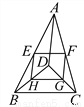
(2)分别为的中点, 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是__.
 11
【解析】试题解析:∵BD⊥DC,BD=4,CD=3,由勾股定理得,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴HG=BC=EF,EH=FG=AD,
∵AD="6,"
∴EF="HG=2.5,EH=GF=3,"
∴四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11.
11
【解析】试题解析:∵BD⊥DC,BD=4,CD=3,由勾股定理得,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴HG=BC=EF,EH=FG=AD,
∵AD="6,"
∴EF="HG=2.5,EH=GF=3,"
∴四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11. 如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).
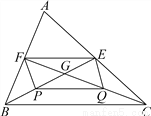
 (1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是...
(1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是... 如图,AC、BD是四边形ABCD的对角线,E、F分别是AD、BC的中点,M、N分别是BD、AC的中点.
求证:EF与MN互相平分.
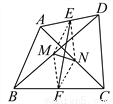
 证明见解析.
【解析】试题分析:连接EM、EN、FM、FN,证明四边形EMFN为平行四边形,根据平行四边形对角线互相平分即可得.
试题解析:连接EM、EN、FM、FN,
∵E为AD的中点,N为AC的中点,
∴EN是△ACD的是位线,
∴EN∥CD,EN=CD,
同理MF∥CD,MF=CD,
∴EN∥MF,EN=MF,
∴四边形EMFN为平行四边形,
...
证明见解析.
【解析】试题分析:连接EM、EN、FM、FN,证明四边形EMFN为平行四边形,根据平行四边形对角线互相平分即可得.
试题解析:连接EM、EN、FM、FN,
∵E为AD的中点,N为AC的中点,
∴EN是△ACD的是位线,
∴EN∥CD,EN=CD,
同理MF∥CD,MF=CD,
∴EN∥MF,EN=MF,
∴四边形EMFN为平行四边形,
... 如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
(1)求证:AE=AF;
(2)求证:BE=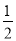 (AB+AC).
(AB+AC).
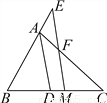
 (1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据角平分线的性质及平行线的性质易∠AEF=∠AFE,即可得AE=AF;(2)作CG∥EM,交BA的延长线于G,已知AC=AG,根据三角形中位线定理的推论证明BE=EG,再利用三角形的中位线定理即可证得结论.
试题解析:
(1)∵DA平分∠BAC,
∴∠BAD=∠CAD,
∵AD∥EM,
∴∠BAD=...
(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据角平分线的性质及平行线的性质易∠AEF=∠AFE,即可得AE=AF;(2)作CG∥EM,交BA的延长线于G,已知AC=AG,根据三角形中位线定理的推论证明BE=EG,再利用三角形的中位线定理即可证得结论.
试题解析:
(1)∵DA平分∠BAC,
∴∠BAD=∠CAD,
∵AD∥EM,
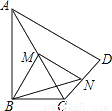
∴∠BAD=... 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
 (1)证明见解析;(2)
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到,再由MN=...
(1)证明见解析;(2)
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到,再由MN=... (1)三角形的中位线的定义:连结三角形两边____________叫做三角形的中位线.
(2)三角形的中位线定理是三角形的中位线________第三边,并且等于___________.
 (1)中点的线段; (2)平行于三角形的 第三边的一半
【解析】(1)三角形的中位线的定义:连结三角形两边中点的线段叫做三角形的中位线,
故答案为:中点的线段;
(2)三角形的中位线定理是三角形的中位线平行于三角形的第三边,并且等于第三边的一半,
故答案为:平行于三角形的,第三边的一半.
(1)中点的线段; (2)平行于三角形的 第三边的一半
【解析】(1)三角形的中位线的定义:连结三角形两边中点的线段叫做三角形的中位线,
故答案为:中点的线段;
(2)三角形的中位线定理是三角形的中位线平行于三角形的第三边,并且等于第三边的一半,
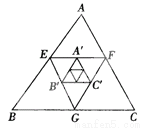
故答案为:平行于三角形的,第三边的一半. 如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.
 16
【解析】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16,
以此类推,第n个小三角形的周长...
16
【解析】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16,
以此类推,第n个小三角形的周长...