题目内容
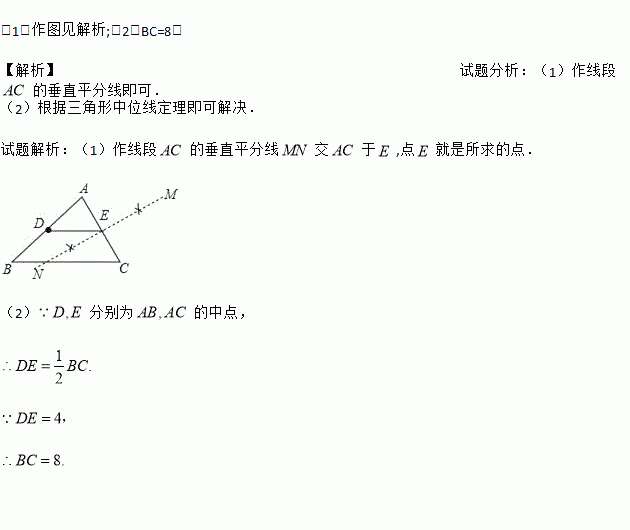
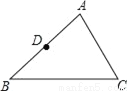
如图，已知△ABC中，D为AB的中点．
（1）请用尺规作图法作边AC的中点E，并连接DE（保留作图痕迹，不要求写作法）；
（2）在（1）的条件下，若DE=4，求BC的长．
（1）作图见解析;（2）BC=8．
【解析】试题分析：（1）作线段的垂直平分线即可．
（2）根据三角形中位线定理即可解决．
试题解析：（1）作线段的垂直平分线交于,点就是所求的点．
（2）分别为的中点，
练习册系列答案
阅读快车系列答案
相关题目
下列说法正确的是（ ）
A. 两个周长相等的长方形全等 B. 两个周长相等的三角形全等
C. 两个面积相等的长方形全等 D. 两个周长相等的圆全等
D
【解析】A.长方形周长相等，但面积、长、宽不一定相等，错；
B.三角形周长相等，但不一定对应边完全相等，错；
C.长方形面积相等，但长、宽不一定相等，错；
D.圆的周长相等，就可知道半径相等，两圆可完全重合，正确。
故选：D. 在五边形ABCDE中，∠A＋∠B＝240°，∠C＝∠D＝∠E＝2∠B.求∠B的度数．
50°
【解析】试题分析：首先求得五边形ABCDE的内角和，设∠B=x°，即可利用x表示其它角的度数，根据多边形的内角和定理即可列方程，从而求得∠B的度数．
试题解析：五边形ABCDE的内角和是（5-2）×180°=540°，
设∠B=x°，则∠C=∠D=∠E=2∠B=2x°，
∵∠A+∠B=240°
∴∠A=240-x°
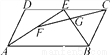
∵∠A+∠B+∠C+∠D+∠E=540... 已知，如图，在?ABCD中，E是CD的中点，F是AE的中点，FC与BE交于点G.求证：GF＝GC.
证明见解析
【解析】试题分析：取BE的中点H，连接FH，CH，利用三角形中位线定理求FH＝AB,利用平行四边形判断定理可得到CEFH是平行四边形，所以GF＝GC.
试题解析：
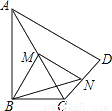
取BE的中点H，连接FH，CH，∵F是AE的中点，∴FH∥AB，FH＝AB.∵CD∥AB，CD＝AB，CE＝CD，∴CE∥FH，且CE＝FH.∴四边形CEFH是平行四边形．∴GF＝GC. 如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．
（1）求证：BM=MN；
（2）∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．
（1）证明见解析；（2）
【解析】试题分析：（1）在△CAD中，由中位线定理得到MN∥AD，且MN=AD，在Rt△ABC中，因为M是AC的中点，故BM=AC，即可得到结论；
（2）由∠BAD=60°且AC平分∠BAD，得到∠BAC=∠DAC=30°，由（1）知，BM=AC=AM=MC，得到∠BMC =60°．由平行线性质得到∠NMC=∠DAC=30°，故∠BMN90°，得到，再由MN=... 在△ABC中，点D、E分别是边AB、AC的中点，那么△ADE的面积与△ABC的面积的比是______.
1∶4
【解析】如图，∵AD=DB，AE=EC，
∴DE∥BC．DE=BC，
∴△ADE∽△ABC，
∴，
故答案为． 有一个两位数，个位上的数字为a，十位上的数字为b，如果把这个两位数的个位与十位上的数字对调，得到的两位数大于原来的两位数，那么a与b哪个大？
a＞b
【解析】试题分析：根据题意得到不等式10b+a＜10a+b，通过解该不等式即可比较它们的大小．
试题解析：根据题意，得
10b+a＜10a+b，
所以，9b＜9a，
所以，b＜a，即a＞b． 将△ABC的∠C折起，翻折后角的顶点位置记作C′，当C′落在AC上时（如图1），易证：∠1=2∠2.
当C′点落在CA和CB之间（如图2）时，或当C′落在CB、CA的同旁（如图3）时，∠1、∠2、∠3关系又如何？请写出你的猜想，并就其中一种情况给出证明.
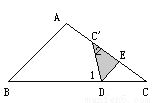
图1 图2 图3
见解析
【解析】利用轴对称的知识找出等解即可进行推理判断.
【解析】
当C′点落在CA和CB之间（如图2）时，∠1+∠3=2∠2；
当C′落在CB、CA的同旁（如图3）时，∠1－∠3=2∠2；
对于图2证明如下：
连结CC’，如图4所示，
∵⊿EC’D是由⊿ECD翻折得到的，
∴⊿EC’D≌⊿ECD，由此得EC=EC’，DC=DC’，∠EC’D=∠ECD... 两个图形关于某直线对称，对称点一定( )
A. 这直线的两旁 B. 这直线的同旁 C. 这直线上 D. 这直线两旁或这直线上
D
【解析】由成轴对称的定义知，成轴对称的两个图形的对称点，或者在对称轴上，或者在对称轴两旁.
故选D.