题目内容
如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).
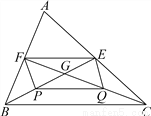
 (1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是...
(1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是...
 心算口算巧算一课一练系列答案
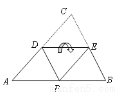
心算口算巧算一课一练系列答案如图,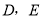 分别为
分别为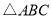 的
的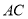 ,
,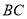 边的中点,将此三角形沿
边的中点,将此三角形沿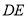 折叠,使点
折叠,使点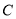 落在
落在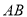 边上的点
边上的点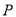 处.若
处.若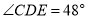 ,则
,则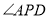 等于( )
等于( )
A.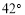 B.
B.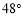 C.
C.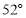 D.
D.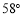
 B
【解析】
试题分析:因为分别为的,边的中点,所以DE是的中位线
所以DE∥BC,所以∠APD=∠EDP,由折叠可知:∠EDP =,所以=.
B
【解析】
试题分析:因为分别为的,边的中点,所以DE是的中位线
所以DE∥BC,所以∠APD=∠EDP,由折叠可知:∠EDP =,所以=. 下列不等式变形正确的是( )
A. 由a>b得ac>bc B. 由a>b得﹣2a>﹣2b
C. 由a>b得﹣a<﹣b D. 由a>b得a﹣2<b﹣2
 B
【解析】试题解析:∵a>b,
∴①c>0时,ac>bc;②c=0时,ac=bc;③c<0时,ac<bc,
∴选项A不正确;
∵a>b,
∴-2a<-2b,
∴选项B不正确;
∵a>b,
∴-a<-b,
∴选项C正确;
∵a>b,
∴a-2>b-2,
∴选项D不正确.
故选C.
B
【解析】试题解析:∵a>b,
∴①c>0时,ac>bc;②c=0时,ac=bc;③c<0时,ac<bc,
∴选项A不正确;
∵a>b,
∴-2a<-2b,
∴选项B不正确;
∵a>b,
∴-a<-b,
∴选项C正确;
∵a>b,
∴a-2>b-2,
∴选项D不正确.
故选C. 已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,求ED.
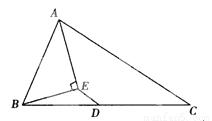
 ED=1.
【解析】延长BE交AC于F,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵BE⊥AE,AE=AE,
∴△ABE≌△AFE,
∴AF=AB,BE=EF,
∵AB=5,
∴AF=5,
∵AC=7,
∴CF=AC-AF=7-5=2,
∵D为BC中点,
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=C...
ED=1.
【解析】延长BE交AC于F,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵BE⊥AE,AE=AE,
∴△ABE≌△AFE,
∴AF=AB,BE=EF,
∵AB=5,
∴AF=5,
∵AC=7,
∴CF=AC-AF=7-5=2,
∵D为BC中点,
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=C... 如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.
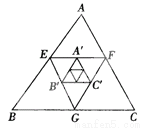
 16
【解析】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16,
以此类推,第n个小三角形的周长...
16
【解析】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16,
以此类推,第n个小三角形的周长... 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
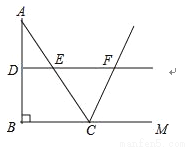
A. 7 B. 8 C. 9 D. 10
 B
【解析】试题分析:在RT△ABC中,∵∠ABC=90°,AB=8,BC=6,∴AC===10,∵DE是△ABC的中位线,∴DF∥BM,DE=BC=3,∴∠EFC=∠FCM,∵∠FCE=∠FCM,∴∠EFC=∠ECF,∴EC=EF=AC=5,∴DF=DE+EF=3+5=8.故选B.
B
【解析】试题分析:在RT△ABC中,∵∠ABC=90°,AB=8,BC=6,∴AC===10,∵DE是△ABC的中位线,∴DF∥BM,DE=BC=3,∴∠EFC=∠FCM,∵∠FCE=∠FCM,∴∠EFC=∠ECF,∴EC=EF=AC=5,∴DF=DE+EF=3+5=8.故选B. 工人小王4月份计划生产零件270个,前 10天平均每天生产5个,后来改进技术,提前3天超额完成任务.设小王10天之后平均每天生产零件x个,请你试着写出x所满足的关系式.
 50+(20-3)x>270
【解析】试题分析:首先设小王10天之后平均每天生产零件x个,利用4月份计划生产零件270个,改进技术后提前3天超额完成任务,进而得出不等式即可.
试题解析:设小王10天之后平均每天生产零件x个,根据题意得
50+(20-3)x>270.
50+(20-3)x>270
【解析】试题分析:首先设小王10天之后平均每天生产零件x个,利用4月份计划生产零件270个,改进技术后提前3天超额完成任务,进而得出不等式即可.
试题解析:设小王10天之后平均每天生产零件x个,根据题意得
50+(20-3)x>270. 下面给出的5个式子中:①3>0,②4x+3y>0,③x=3,④x-1,⑤x+2≤3,其中不等式有( )
A.2个 B.3个 C.4个 D.5个
 B.
【解析】
试题解析:3>0;4x+3y>0;x+2≤3是不等式.
故选B.
B.
【解析】
试题解析:3>0;4x+3y>0;x+2≤3是不等式.
故选B. 下面说法中正确的是( )
A. 设A、B关于直线MN对称,则AB垂直平分MN.
B. 如果△ABC≌△DNF,则一定存在一条直线MN,使△ABC与△DNF关于MN 对称.
C. 如果一个三角形是轴对称图形,且对称轴不止一条,则它是等边三角形.
D. 两个图形关于MN对称,则这两个图形分别在MN的两侧.
 C
【解析】A中应该是直线MN垂直平分线段AB,故错误;
B因为成轴对称的两个图形一定全等,但全等形不一定是轴对称图形,故错误;
C因为等边三角形是轴对称图形,且有3条对称轴,故正确;
D中错在这两个图形不一定要在直线两侧,同侧也可以有,如下图,故错误.
故选C.
C
【解析】A中应该是直线MN垂直平分线段AB,故错误;
B因为成轴对称的两个图形一定全等,但全等形不一定是轴对称图形,故错误;
C因为等边三角形是轴对称图形,且有3条对称轴,故正确;
D中错在这两个图形不一定要在直线两侧,同侧也可以有,如下图,故错误.
故选C. 
