题目内容
如图，D是△ABC内一点，BD⊥CD，AD＝6，BD＝4，CD＝3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是__.
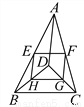
11
【解析】试题解析：∵BD⊥DC，BD=4，CD=3，由勾股定理得，
∵E、F、G、H分别是AB、AC、CD、BD的中点，
∴HG=BC=EF，EH=FG=AD，
∵AD="6，"
∴EF="HG=2.5，EH=GF=3，"
∴四边形EFGH的周长是EF+FG+HG+EH=2×（2.5+3）=11．
练习册系列答案
相关题目
使两个直角三角形全等的条件是（ ）
A. 一锐角对应相等 B. 两锐角对应相等 C. 一条边对应相等 D. 两条边对应相等
D
【解析】试题分析：利用全等三角形的判定来确定．做题时，要结合已知条件与三角形全等的判定方法逐个验证．
【解析】
A、一个锐角对应相等，利用已知的直角相等，可得出另一组锐角相等，但不能证明两三角形全等，故A选项错误；
B、两个锐角相等，那么也就是三个对应角相等，但不能证明两三角形全等，故B选项错误；
C、一条边对应相等，再加一组直角相等，不能得出两三角形全等，故C选项错... 若x＞y，则下列式子中错误的是( )
A. x－3＞y－3 B. x＋3＞y＋3
C. －3x＞－3y D.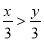 
C
【解析】试题分析：A、不等式的两边都减3，不等号的方向不变，故A正确；
B、不等式的两边都加3，不等号方向不变，故B正确；
C、不等式的两边都乘-3，不等号的方向改变，故C错误；
D、不等式的两边都除以3，不等号的方向改变，故D正确；
故选C． 已知：如图，在四边形ABCD中，AD＝BC，E、F分别是DC、AB边的中点，FE的延长线分别与AD、BC的延长线交于H、G点．求证：∠AHF＝∠BGF．
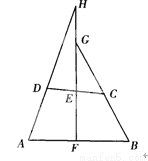
证明见解析.
【解析】试题分析：连接AC，取AC中点为M，连接ME、MF，根据中位线定理证明EM=MF，从而可得∠MEF=∠MFE，根据平行线同位角相等，证明∠MEF=∠AHF，∠MFE=∠BGF，可以求证∠AHF=∠BGF．
试题解析：连接AC，取AC中点为M，连接ME、MF，如图：
∵E是CD的中点，M为AC中点，
∴EM∥AD，且EM=AD，
∵M是AC的中点，... (1)三角形的中位线的定义：连结三角形两边____________叫做三角形的中位线．
(2)三角形的中位线定理是三角形的中位线________第三边，并且等于___________．
(1)中点的线段; (2)平行于三角形的 第三边的一半
【解析】(1)三角形的中位线的定义：连结三角形两边中点的线段叫做三角形的中位线，
故答案为：中点的线段；
(2)三角形的中位线定理是三角形的中位线平行于三角形的第三边，并且等于第三边的一半，
故答案为：平行于三角形的，第三边的一半. 如图，在△ABC中，∠ACB=90°，AC=8，AB="10." DE垂直平分AC交AB于点E，则DE的长为（ ）
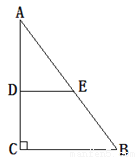
A. 6 B. 5 C. 4 D. 3
D
【解析】试题分析：已知，在△ABC中，∠ACB=90°，AC=8，AB=10，根据勾股定理可得BC=6，又因DE垂直平分AC，∠ACB=90°，可得DE为△ABC的中位线，根据三角形的中位线定理可得DE=BC=3，故答案选D. 某班同学去春游花了250元包租了一辆客车，如果参加春游的同学每人交8元钱租车费，还不够，如果每人交9元，还用不了．用不等式表示出上述问题中存在的不等关系．
见解析
【解析】试题分析：根据每人交8元钱租车费，还不够可得8x＜250；根据如果每人交9元，还用不了可得9x＞250．
试题解析：设参加春游的同学x人，由题意得
. 如图，两条相交直线l1与l2的夹角是45°，都是一个图案的对称轴，画出这个图案的其余部分．这个图案共有多少条对称轴？
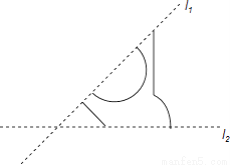
答案见解析.
【解析】试题分析：根据轴对称图形和对称轴的定义即可得到结果.
如图所示：
这个图案共有四条对称轴. 轴对称图形沿对称轴对折后，对称轴两旁的部分( )
A. 完全重合 B. 不完全重合 C. 两者都有 D. 不确定
A
【解析】由轴对称图形的定义知，轴对称图形沿对称轴对折后，对称轴两旁的部分完全重合.
故选A.