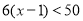题目内容
如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，AD=BC，∠PEF=18°，则∠PFE的度数是 度．
18．
【解析】
试题分析：根据中位线定理和已知，易证明△EPF是等腰三角形．∵在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，∴FP，PE分别是△CDB与△DAB的中位线，∴PF=BC，PE=AD，∵AD=BC，∴PF=PE，故△EPF是等腰三角形．∵∠PEF=18°，∴∠PEF=∠PFE=18°．故答案为：18．
练习册系列答案
阅读快车系列答案
相关题目
在下列条件中，不能说明△ABC≌△A’B’C’的是( )
A. ∠A＝∠A’，∠C＝∠C’，AC＝A’C’ B. ∠A＝∠A’，AB＝A’B’，BC＝B’C’
C. ∠B＝∠B’，∠C＝∠C’，AB＝A’B’ D. AB＝A’B’， BC＝B’ C’AC＝A’C’
B
【解析】A、∠A=∠A′，∠C=∠C′，AC=A′C′，可用ASA判定△ABC≌△A′B′C，故选项正确；
B、∠A=∠A′，AB=A′B′，BC=B′C′，SSA不能判定两个三角形全等，故选项错误；
C、∠B=∠B′，∠C=∠C′，AB=A′B′，可用AAS判定△ABC≌△A′B′C，故选项正确；
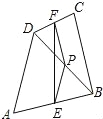
D、AB=A′B′，BC=B′C，AC=A′C′，可用ASA判定△AB... 如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角.若∠A＝120°，则∠1＋∠2＋∠3＋∠4＝ .
300°
【解析】由题意得，∠5＝180°－∠EAB＝60°
，
又∵多边形的外角和为360°，
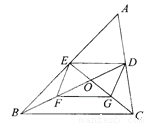
∴∠1＋∠2＋∠3＋∠4＝360°－∠5＝300°. 已知：△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．求证：四边形DEFG是平行四边形．
证明见解析.
【解析】试题分析：根据BD，CE是△ABC的中线可得DE是△ABC的中位线，F，G分别是OB，OC的中点可得FG是△BOC的中位线，根据三角形中位线定理可得DE∥BC且DE=BC，FG∥BC且FG=BC，进而可得DE∥FG且DE=FG，根据一组对边平行且相等的四边形是平行四边形可得结论.
试题解析：∵BD、CE是△ABC的中线，∴DE是△ABC的中位线，
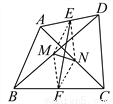
∴DE∥B... 如图，AC、BD是四边形ABCD的对角线，E、F分别是AD、BC的中点，M、N分别是BD、AC的中点．
求证：EF与MN互相平分．
证明见解析.
【解析】试题分析：连接EM、EN、FM、FN，证明四边形EMFN为平行四边形，根据平行四边形对角线互相平分即可得.
试题解析：连接EM、EN、FM、FN，
∵E为AD的中点，N为AC的中点，
∴EN是△ACD的是位线，
∴EN∥CD，EN＝CD，
同理MF∥CD，MF＝CD，
∴EN∥MF，EN＝MF，
∴四边形EMFN为平行四边形，
... 班级50名学生上体育课，老师出了一道题目：现在我拿来一些篮球，如果每5人一组玩一个篮球，有些同学没有球玩；如果每6人一组玩一个篮球，就会有一组玩篮球的人数不足6个．你们知道有几个篮球吗？
甲同学说：如果有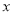
个篮球，
．
乙同学说：
．
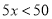丙同学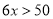说：
．
你明白他们的意思吗？
甲同学说的意思是：如果每5人一组玩一个篮球，那么玩球的人数少于50人，有些同学就没有球玩．
乙同学说的意思是：如果每6人一组玩一个篮球，那么就会有一个组玩篮球的人数不足6人．
丙同学说的意思是：如果每6人一组玩一个篮球，除了一个球以外，剩下的每6人玩一个球，还有几个（不足6人）玩另外一个篮球．
【解析】
试题分析：
甲同学说的意思是：如果每5人一组玩一个篮球，那么玩球... 用不等式表示下列关系：
（1）一个数的平方是非负数；（2）某天的气温不高于 25℃．
（1）x2≥0；（2）x≤25．
【解析】试题分析：（1）非负数则表示为“大于或等于0的数”；
（2）不高于则表示为“小于或等于”，用数学符号表示即可．
试题解析：（1）设这个数为x，则x2≥0；
（2）设某天的气温为x℃， 则x≤25． 用四块如图所示的两色正方形瓷砖，拼成一个新的正方形，使拼成轴对称图案，请至少给出三种不同的拼法：
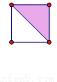
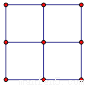
见解析
【解析】根据轴对称的概念进行图形设计即可.
【解析】
根据轴对称要求，设计出利用两色磁砖拼成的正方形如图所示. 如果一个三角形是轴对称图形，且有一个内角是60°,那么这个三角形是( )
A. 等边三角形 B. 等腰直角三角形 C. 等腰三角形 D. 含30°角的直角三角形
A
【解析】∵这个三角形是轴对称图形 ，
∴一定有两个角相等，
∴这是一个等腰三角形.
∵有一个内角是60°，
∴这个三角形是等边三角形.
故选A.