题目内容
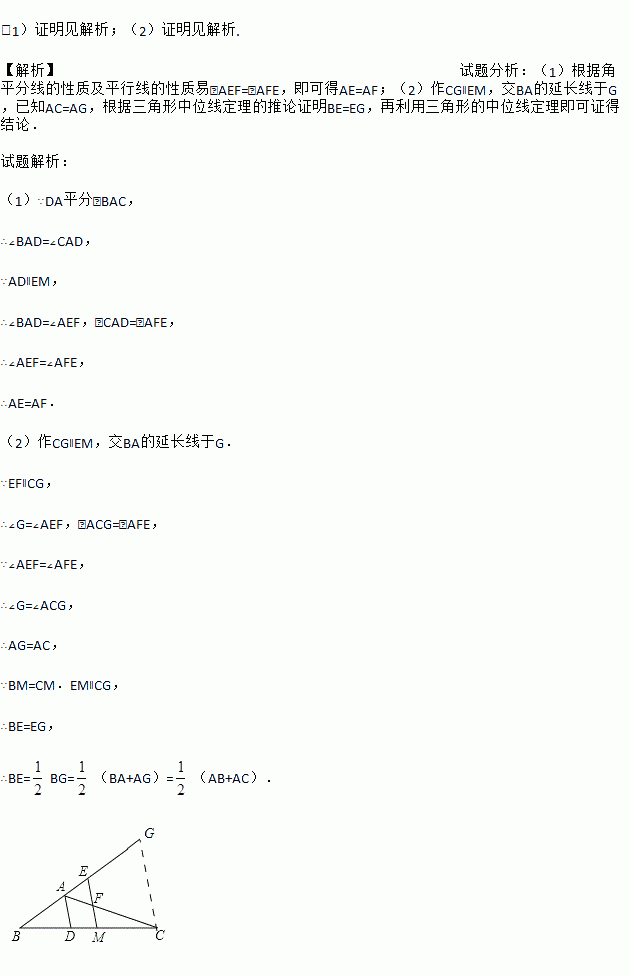
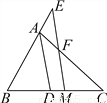
如图，已知△ABC，AD平分∠BAC交BC于点D，BC的中点为M，ME∥AD，交BA的延长线于点E，交AC于点F.
(1)求证：AE＝AF；
(2)求证：BE＝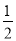
(AB＋AC)．
（1）证明见解析；（2）证明见解析.
【解析】试题分析：（1）根据角平分线的性质及平行线的性质易∠AEF=∠AFE，即可得AE=AF；（2）作CG∥EM，交BA的延长线于G，已知AC=AG，根据三角形中位线定理的推论证明BE=EG，再利用三角形的中位线定理即可证得结论．
试题解析：
（1）∵DA平分∠BAC，
∴∠BAD=∠CAD，
∵AD∥EM，
∴∠BAD=...
练习册系列答案
相关题目
已知:如图,AC=CD ,∠B=∠E=90°, AC⊥CD,则不正确的结论是 ( )
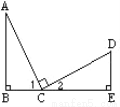
A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△CED D. ∠1=∠2
D
【解析】∵AC⊥CD，
∴∠1+∠2=90°，
∵∠B=90°，
∴∠1+∠A=90°，
∴∠A=∠2，
在△ABC和△CED中，
，
∴△ABC≌△CED(AAS)，
故B、C选项正确；
∵∠2+∠D=90°，
∴∠A+∠D=90°，
故A选项正确；
∵AC⊥CD，
∴∠ACD=90°，
∠1+∠2=... 因为－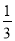
x＞1，所以x____－3(填“＞”或“＜”)，依据是__________________.
< 不等式的基本性质3
【解析】不等式两边同时乘以-3得，x＜-3，
故答案为：<，不等式的基本性质3． 过多边形的一个顶点的所有对角线把多边形分成8个三角形，这个多边形的边数是( )
A. 8 B. 9 C. 10 D. 11
C
【解析】设多边形有n条边，
则n-2=8，解得n=10，
所以这个多边形的边数是10，
故选C. 如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，求证：四边形EFGH是平行四边形。
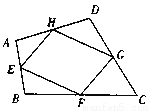
证明见解析
【解析】试题分析：连接AC，根据三角形的中位线的性质证得线段平行且相等，从而根据平行四边形的判定（一组对边平行且相等的四边形是平行四边形）得证.
试题解析：证明：连接AC
∵E，F，G，H是四边形ABCD的中点
∴EF，HG分别是△BCA和△DCA的中位线
∴EF∥AC，HG∥AC，且EF=
∴EF∥HG， EF=HG
∴四边形EFGH是平行四... 如图，?ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD＝12，求△DOE的周长．
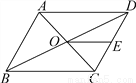
△DOE的周长为15.
【解析】试题分析：根据平行四边形的对边相等和对角线互相平分可得，OB=OD，又因为E点是CD的中点，可得OE是△BCD的中位线，可得OE=BC，所以易求△DOE的周长．
试题解析：∵平行四边形ABCD的周长为36，
∴2（BC+CD）=36，则BC+CD=18．
∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，BD=12，
∴OD=O... 比较下面每小题中两个算式结果的大小(在横线上填“＞”、“＜”或“＝”)．
⑴32＋42 2×3×4；⑵22＋22 2×2×2；⑶12＋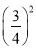
2×1×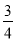
；
⑷(－2) 2＋52 2×(－2)×5；⑸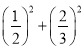
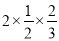
通过观察上面的算式，请你用字母来表示上面算式中反映的一般规律．
(1）＞（2）＝（3）＞（4）＞（5）＞； ≥2ab（当a＝b时取等号）．
【解析】试题分析：分别根据有理数的乘方法则求出各数的值，再根据有理数比较大小的法则比较出各数的大小，并总结出规律．
试题解析：（1）∵32+42=25，2×3×4=24，
∴32+42＞2×3×4；
（2）∵22+22=8，2×2×2=8，
∴22+22=2×2×2；
（3）∵12+()... a是非负数的表达式是（ ）
A. a＞0 B. 
≥0 C. a≤0 D. a≥0
D
【解析】非负数是指大于或等于0的数，所以a≥0，
故选D. 下列推理中，错误的是( )
A. ∵∠A＝∠B＝∠C，∴△ABC是等边三角形
B. ∵AB＝AC，且∠B＝∠C，∴△ABC是等边三角形
C. ∵∠A＝60°，∠B＝60°，∴△ABC是等边三角形
D. ∵AB＝AC，∠B＝60°，∴△ABC是等边三角形
B
【解析】A∵∠A＝∠B＝∠C，∴△ABC是等边三角形，故正确；
B条件重复且条件不足，故不正确；
C∵∠A＝60°，∠B＝60°，∴∠C=60°，∴△ABC是等边三角形60°，故正确；
D根据有一个角是60°的等腰三角形是等边三角形可以得到，故正确.
故选B.