题目内容
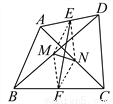
如图，AC、BD是四边形ABCD的对角线，E、F分别是AD、BC的中点，M、N分别是BD、AC的中点．
求证：EF与MN互相平分．
证明见解析.
【解析】试题分析：连接EM、EN、FM、FN，证明四边形EMFN为平行四边形，根据平行四边形对角线互相平分即可得.
试题解析：连接EM、EN、FM、FN，
∵E为AD的中点，N为AC的中点，
∴EN是△ACD的是位线，
∴EN∥CD，EN＝CD，
同理MF∥CD，MF＝CD，
∴EN∥MF，EN＝MF，
∴四边形EMFN为平行四边形，
...
练习册系列答案
开心蛙口算题卡系列答案
相关题目
如图，△ABC≌△CDA,且AD＝CB，下列结论错误的是（ ）
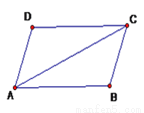
A. ∠B＝∠D B. ∠CAB＝∠ACD C. BC＝CD D. AC＝CA
C
【解析】∵△ABC≌△CDA，
∴∠CAB＝∠ACD，CA=AC，∠D=∠B，故A. B.D正确，不符合题意，
BC不一定等于CD，C错误，符合题意，
故选：C. 下列变形中，不正确的是( )
A. 由x－5＞0可得x＞5
B. 由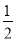
x＞0可得x＞0
C. 由－3x＞－9可得x＞3
D. 由－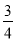
x＞1可得x＜－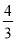
C
【解析】A、在不等式两边同加上5，不等号不变，故正确；B、在不等式的两边同时乘以2，不等号不变，故正确；C、在不等式的两边同时除以-3，不等号方向改变，故错误；D、在不等式的两边同时乘以一个负数，不等号方向改变，故正确，
故先C． 如图在△ABC中，D、E分别为AB、AC上的点，且BD＝CE，M、N分别是BE、CD的中点．过MN的直线交AB于P，交AC于Q，线段AP、AQ相等吗?为什么?
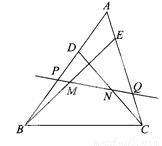
AP=AQ，理由见解析.
【解析】根据中位线定理证明MH=NH，进而证明∠HMN=∠HNM，∠HMN=∠PQA，所以△APQ为等腰三角形，即AP=AQ． △ABC中，D、E分别为AB、AC的中点，若DE＝4，AD＝3，AE＝2，则△ABC的周长为______．
18
【解析】∵点D，E分别是△ABC的边AB，AC的中点，
∴DE是△ABC的中位线，
∴AB=2AD=2×3=6，AC=2AE＝2×2=4，BC=2DE=2×4=8，
∴AB+AC+BC=18，
即△ABC的周长为18，
故答案为：18. 如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，AD=BC，∠PEF=18°，则∠PFE的度数是 度．
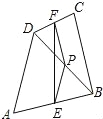
18．
【解析】
试题分析：根据中位线定理和已知，易证明△EPF是等腰三角形．∵在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，∴FP，PE分别是△CDB与△DAB的中位线，∴PF=BC，PE=AD，∵AD=BC，∴PF=PE，故△EPF是等腰三角形．∵∠PEF=18°，∴∠PEF=∠PFE=18°．故答案为：18． 某次数学测验，共有16道选择题，评分方法是：答对一题得6分，不答或答错一题扣2分．某同学要想得分为60分以上，他至少应答对多少道题?(只列关系式)
6x－2(16－x)≥60
【解析】试题分析：关系式为：6×答对的题数-2×其余题数≥60，据此列不等式即可.
试题解析：设该同学应答对x道题，依题意得
6x－2(16－x) ≥60. a、b两数在数轴上的位置如图所示，下列结论中正确的是（ ）
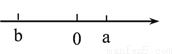
A. a＞0，b＜0 B. a＜0，b＞0 C. ab＞0 D. 以上均不对
A
【解析】观察数轴可知a>0，b<0，a>b，所以ab<0，
故选A.