��Ŀ����
(1)�����ε���λ�ߵĶ��壺��������������____________���������ε���λ�ߣ�
(2)�����ε���λ�߶����������ε���λ��________�����ߣ����ҵ���___________��
 (1)�е���߶�; (2)ƽ���������ε� �����ߵ�һ��
��������(1)�����ε���λ�ߵĶ��壺���������������е���߶ν��������ε���λ�ߣ�
�ʴ�Ϊ���е���߶Σ�
(2)�����ε���λ�߶����������ε���λ��ƽ���������εĵ����ߣ����ҵ��ڵ����ߵ�һ�룬
�ʴ�Ϊ��ƽ���������εģ������ߵ�һ��.
(1)�е���߶�; (2)ƽ���������ε� �����ߵ�һ��
��������(1)�����ε���λ�ߵĶ��壺���������������е���߶ν��������ε���λ�ߣ�
�ʴ�Ϊ���е���߶Σ�
(2)�����ε���λ�߶����������ε���λ��ƽ���������εĵ����ߣ����ҵ��ڵ����ߵ�һ�룬
�ʴ�Ϊ��ƽ���������εģ������ߵ�һ��.
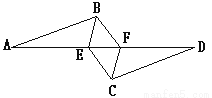
��ͼ����֪AB��CD��AB=CD,AE=FD,��ͼ�е�ȫ���������У� ��
A. 1�� B. 2�� C. 3�� D. 4��
 C
����������AB��CD��
���A=��D��
��AB=CD��AE=FD��
���ABE�ա�DCF(SAS)��
��BE=CF����BEA=��CFD��
���BEF=��CFE��
��EF=FE��
���BEF�ա�CFE(SAS)��
��BF=CE��
��AE=DF��
��AE+EF=DF+EF��
��AF=DE��
���ABF�ա�CDE(SSS)...
C
����������AB��CD��
���A=��D��
��AB=CD��AE=FD��
���ABE�ա�DCF(SAS)��
��BE=CF����BEA=��CFD��
���BEF=��CFE��
��EF=FE��
���BEF�ա�CFE(SAS)��
��BF=CE��
��AE=DF��
��AE+EF=DF+EF��
��AF=DE��
���ABF�ա�CDE(SSS)... �Ѳ���ʽ2x��3��x��Ϊx��a��x��a����ʽ��( )
A. x��3 B. x��3
C. x��1 D. x��1
 C
��������2x��3��x��
����ͬʱ����x��
2x+x>3��
3x>3��
����ͬʱ����3��
x>1��
��ѡC.
C
��������2x��3��x��
����ͬʱ����x��
2x+x>3��
3x>3��
����ͬʱ����3��
x>1��
��ѡC. ��n�����ڽǺ�Ϊ900�㣬�����n= ��
 7��
��������
�����������������ã�180��n��2��=900����ã�n=7���ʴ�Ϊ��7��
7��
��������
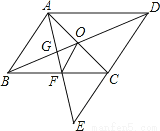
�����������������ã�180��n��2��=900����ã�n=7���ʴ�Ϊ��7�� ��֪����ͼ��EΪ��ABCD��DC�ߵ��ӳ����ϵ�һ�㣬��CE��DC������AE�ֱ�BC��BD�ڵ�F��G������AC��BD��O������OF����֤��AB��2OF��
 ֤��������.
��������
�����������֤����ABF�ա�ECF��BF=FC����������������λ�߶������ɽ�����⣮
������������ı���ABCD��ƽ���ı��Σ�
��AB=CD��AB��CD��AO=OC��
��CD=CE��
��AB=CE����BAF=��CEF��
�ڡ�ABF�͡�ECF�У�
��
���ABF�ա�ECF��
��BF=FC��
��AO=OC��
...
֤��������.
��������
�����������֤����ABF�ա�ECF��BF=FC����������������λ�߶������ɽ�����⣮
������������ı���ABCD��ƽ���ı��Σ�
��AB=CD��AB��CD��AO=OC��
��CD=CE��
��AB=CE����BAF=��CEF��
�ڡ�ABF�͡�ECF�У�
��
���ABF�ա�ECF��
��BF=FC��
��AO=OC��
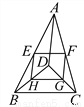
... ��ͼ��D�ǡ�ABC��һ�㣬BD��CD��AD��6��BD��4��CD��3��E��F��G��H�ֱ���AB��AC��CD��BD���е㣬���ı���EFGH���ܳ���__.
 11
�������������������BD��DC��BD=4��CD=3���ɹ��ɶ����ã�
��E��F��G��H�ֱ���AB��AC��CD��BD���е㣬
��HG=BC=EF��EH=FG=AD��
��AD="6��"
��EF="HG=2.5��EH=GF=3��"
���ı���EFGH���ܳ���EF+FG+HG+EH=2����2.5+3��=11��
11
�������������������BD��DC��BD=4��CD=3���ɹ��ɶ����ã�
��E��F��G��H�ֱ���AB��AC��CD��BD���е㣬
��HG=BC=EF��EH=FG=AD��
��AD="6��"
��EF="HG=2.5��EH=GF=3��"
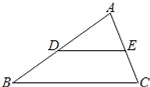
���ı���EFGH���ܳ���EF+FG+HG+EH=2����2.5+3��=11�� ��ͼ���ڡ�ABC�У�D��E�ֱ��DZ�AB��AC���е㣬BC=8����DE= ��
 4
�������������������֪D��E�ֱ��DZ�AB��AC���е㣬BC=8�����������ε���λ�߶����õ�DE=BC=4��
4
�������������������֪D��E�ֱ��DZ�AB��AC���е㣬BC=8�����������ε���λ�߶����õ�DE=BC=4�� С����ˮ��̯�ϳ���2��ƻ����̯�����˼���ƻ��˵�����㿴�ӣ��߸ߵģ��������ƻ����ʵ������Ϊx��ò���ʽ��������߸ߵġ�����˼��ʾ�����ǣ� ��
A.x��2 B.x��2 C.x��2 D.x��2
 C
��������
�������������������
�߸ߵ���˼˵�ȱ��������ߣ�
��������
�����⣺x��2��
��ѡC��
C
��������
�������������������
�߸ߵ���˼˵�ȱ��������ߣ�
��������
�����⣺x��2��
��ѡC�� ��ABC�У�AB��AC����D�붥��A��ֱ��BCͬ�࣬��BD��AD����BD��CD�Ĵ�С��ϵΪ( )
A. BD��CD B. BD��CD C. BD��CD D. BD��CD��С��ϵ��ȷ��
 D
������������ͼ��Ӧ�������������(1) BD��CD��(2) BD��CD ��3) BD��CD.
��ѡD
D
������������ͼ��Ӧ�������������(1) BD��CD��(2) BD��CD ��3) BD��CD.
��ѡD 
