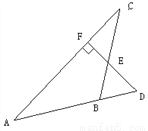
如图所示，D为△ABC的边AB的延长线上一点，过D作DF⊥AC，垂足为F，交BC于E,且BD=BE,求证：△ABC是等腰三角形.
证明见解析
【解析】试题分析：可用逆推法，欲证△ABC是等腰三角形，由图可知应证AB=BC，由“等角对等边”，应想到只要证∠A=∠C．由角的互余关系可知∠A＋∠D=90°，∠C＋∠CEF=90°，∠CEF =∠BED，由BD=BE可知∠BED=∠D，可得∠A=∠C，本题得证．
试题解析：∵BD＝BE，∴∠BDE＝∠BED，
又∵∠BED＝∠CEF，∴∠BDE＝∠CEF，
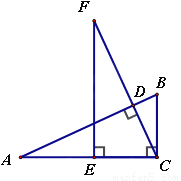
又... 如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，CE=BC，过点E作AC的垂线，交CD的延长线于点F．求证：AB=FC．
见解析证明．
【解析】
试题分析：利用同角的余角相等得到一对角相等，再由一对直角相等，夹边EC=BC，利用AAS得到△FEC与△ACB全等，利用全等三角形对应边相等即可得证．
试题解析：∵EF⊥AC，∴∠FEC=90°=∠ACB，∴∠F +∠FCE= 90°，∵CD⊥AB，∴∠ADC=90°，∴∠A +∠FCE =90°， ∴∠F=∠A，在△FEC和△ACB中，∵，∴△FEC≌△... 下列说法中不正确的是（ ）
A. 平行四边形是中心对称图形
B. 斜边及一锐角分别相等的两直角三角形全等
C. 两个锐角分别相等的两直角三角形全等
D. 一直角边及斜边分别相等的两直角三角形全等
C
【解析】解：A．平行四边形是中心对称图形，说法正确；
B．斜边及一锐角分别相等的两直角三角形全等，说法正确；
C．两个锐角分别相等的两直角三角形全等，说法错误；
D．一直角边及斜边分别相等的两直角三角形全等，说法正确．
故选C． 将一副直角三角尺如图放置，若∠AOD=20°， 则∠BOC的大小为（ ）
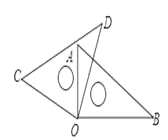
A. 140° B. 160° C. 170° D. 150°
B
【解析】试题分析：根据∠AOD=20°可得：∠AOC=70°，根据题意可得：∠BOC=∠AOB+∠AOC=90°+70°=160°. Rt△ABC中，∠C=90°，∠B=46°，则∠A=（ ）
A. 44° B. 34° C. 54° D. 64°
A
【解析】【解析】
∵∠C=90°，∠B=46°，∴∠A=90°﹣46°=44°．故选A． 如图，一个矩形纸片，剪去部分后得到一个三角形，则图中∠1+∠2的度数是（ ）
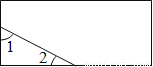
A. 30° B. 60° C. 90° D. 120°
C
【解析】试题分析：由题意得，剩下的三角形是直角三角形，
所以，∠1+∠2=90°．
故选C． 如图，若要用“HL”证明Rt△ABC≌Rt△ABD，则还需补充条件（ ）
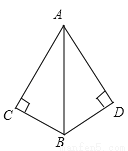
A. ∠BAC=∠BAD B. AC=AD或BC=BD
C. AC=AD且BC=BD D. 以上都不正确
B
【解析】试题解析：从图中可知AB为Rt△ABC和Rt△ABD的斜边，也是公共边．
很据“HL”定理，证明Rt△ABC≌Rt△ABD，
还需补充一对直角边相等，
即AC=AD或BC=BD，
故选B． 下列可使两个直角三角形全等的条件是（ ）
A. 一条边对应相等 B. 两条直角边对应相等
C. 一个锐角对应相等 D. 两个锐角对应相等
B
【解析】【解析】
两直角三角形隐含一个条件是两直角相等，要判定两直角三角形全等，起码还要两个条件，故可排除A、C；
而D构成了AAA，不能判定全等；
B构成了SAS，可以判定两个直角三角形全等．
故选B． 如图，O是∠BAC内一点，且点O到AB，AC的距离OE=OF，则△AEO≌△AFO的依据是（ ）
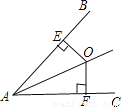
A.HL B.AAS C.SSS D.ASA
A
【解析】
试题分析：利用点O到AB，AC的距离OE=OF，可知△AEO和△AFO是直角三角形，然后可直接利用HL求证△AEO≌△AFO，即可得出答案．
【解析】
∵OE⊥AB，OF⊥AC，∴∠AEO=∠AFO=90°，
又∵OE=OF，AO为公共边，∴△AEO≌△AFO．
故选A． 如图所示，AB⊥BD，AC⊥CD，∠D=35°，则∠A的度数为（ ）
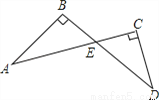
A. 65° B. 35° C. 55° D. 45°
B
【解析】【解析】
∵AB⊥BD，AC⊥CD，∴∠B=∠C=90°，∴∠A+∠AEB=∠D+∠CED=90°．
又∵∠AEB=∠CED，∴∠A=∠D=35°．故选B．