��Ŀ����
��ͼ���ڡ�ABC�У���ACB=90�㣬CD��AB�ڵ�D����E��AC�ϣ�CE=BC������E��AC�Ĵ��ߣ���CD���ӳ����ڵ�F����֤��AB=FC��
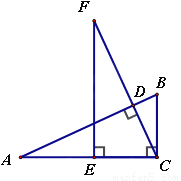
 ������֤����
��������
�������������ͬ�ǵ������ȵõ�һ�Խ���ȣ�����һ��ֱ����ȣ��б�EC=BC������AAS�õ���FEC���ACBȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤��
�����������EF��AC�����FEC=90��=��ACB�����F +��FCE= 90�㣬��CD��AB�����ADC=90�㣬���A +��FCE =90�㣬 ���F=��A���ڡ�FEC�͡�ACB�У��ߣ����FEC�ա�...
������֤����
��������
�������������ͬ�ǵ������ȵõ�һ�Խ���ȣ�����һ��ֱ����ȣ��б�EC=BC������AAS�õ���FEC���ACBȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤��
�����������EF��AC�����FEC=90��=��ACB�����F +��FCE= 90�㣬��CD��AB�����ADC=90�㣬���A +��FCE =90�㣬 ���F=��A���ڡ�FEC�͡�ACB�У��ߣ����FEC�ա�...
 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д���ͼ��ʾ��һ������б����ǽ�ϣ������ӵ˵�ǽ�ľ���AC=3�ף�cos��BAC��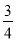 ��������AB�ij���Ϊ______�ף�
��������AB�ij���Ϊ______�ף�
 4
����������Rt��BCA�У�AC��3�ף�cos��BAC��������AB��4�ף������ӵij���Ϊ4�ף�
4
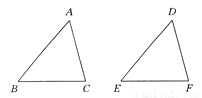
����������Rt��BCA�У�AC��3�ף�cos��BAC��������AB��4�ף������ӵij���Ϊ4�ף� ��ͼ��ʾ����DEF���ɡ�ABC����ƽ�Ƶõ��ģ�����B=50��,��C=75��,���D=_____����E��________.
 55�� 50��
������������������ڡ�ABC�У���A��180�㣭��B����C��55�㣬
��ƽ�Ƶ����ʿ�֪����D����A��55�㣬��E����B��50�㣬
�ʴ�Ϊ��55�㣬50�㣮
55�� 50��
������������������ڡ�ABC�У���A��180�㣭��B����C��55�㣬
��ƽ�Ƶ����ʿ�֪����D����A��55�㣬��E����B��50�㣬
�ʴ�Ϊ��55�㣬50�㣮 �������ֱ�������ε�����ֱ�DZ߶�Ӧ��ȣ���ô������ֱ��������ȫ�ȵ������ǣ�������
A. SSS B. AAS C. SAS D. HL
 C
����������������
�����нǶ�Ӧ��ȵ�����������ȫ�ȣ���Ϊ���߽DZߡ���������д�ɡ�SAS������ѡC��
C
����������������
�����нǶ�Ӧ��ȵ�����������ȫ�ȣ���Ϊ���߽DZߡ���������д�ɡ�SAS������ѡC�� ��ͼ����Ҫ�á�HL��֤��Rt��ABC��Rt��ABD�����貹�������� ��
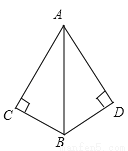
A. ��BAC=��BAD B. AC=AD��BC=BD
C. AC=AD��BC=BD D. ���϶�����ȷ
 B
�������������������ͼ�п�֪ABΪRt��ABC��Rt��ABD��б�ߣ�Ҳ�ǹ����ߣ�
�ܾݡ�HL��������֤��Rt��ABC��Rt��ABD��
���貹��һ��ֱ�DZ���ȣ�
��AC=AD��BC=BD��
��ѡB��
B
�������������������ͼ�п�֪ABΪRt��ABC��Rt��ABD��б�ߣ�Ҳ�ǹ����ߣ�
�ܾݡ�HL��������֤��Rt��ABC��Rt��ABD��
���貹��һ��ֱ�DZ���ȣ�
��AC=AD��BC=BD��
��ѡB�� ���������εĶ��Ǧ���90�㣬������䶥�ǵĶ�����һ��ֱ�߽�������������η� �����������������Σ���ô���Ķ���Ϊ________��
 108��
����������ͼ��
��AB=AC��BD=AD��AC=CD��
���1=��B����2=��4����B=��C��
�ߡ�4=��1+��B=2��B=2��C��
���2=��4=2��C��
�ߡ�2+��4+��C=180�㣬
��5��C=180�㣬
���C=36�㣬
���=��BAC=180��-2��C=108�㣮
108��
����������ͼ��
��AB=AC��BD=AD��AC=CD��
���1=��B����2=��4����B=��C��
�ߡ�4=��1+��B=2��B=2��C��
���2=��4=2��C��
�ߡ�2+��4+��C=180�㣬
��5��C=180�㣬
���C=36�㣬
���=��BAC=180��-2��C=108�㣮 ������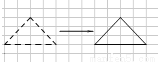 �ұߵ�������ߵ�����ƽ�Ƶõ��ģ�
�ұߵ�������ߵ�����ƽ�Ƶõ��ģ�
 ����ƽ��7����λ.
���������������:�۲�ͼ���ж�Ӧ��ı仯�����ɵó�ͼ�εı仯����.
���������
�ҳ���Ӧ������ᷢ���ұߵ�ͼ��������ߵ�����ƽ��7����λ���ȵõ���.
����ƽ��7����λ.
���������������:�۲�ͼ���ж�Ӧ��ı仯�����ɵó�ͼ�εı仯����.
���������
�ҳ���Ӧ������ᷢ���ұߵ�ͼ��������ߵ�����ƽ��7����λ���ȵõ���. ��ͼ��ƽ�ƵĹ����У�����˵���д�����ǣ� ��
A. ͼ����������ƶ��ķ�����ͬ B. ͼ����������ƶ��ľ�����ͬ
C. ͼ���Ͽ��ܴ��ڲ����ĵ� D. ͼ���������������ߵij��Ȳ���
 C
�����������������ƽ�Ƶ�ʱ��ͼ���ϵ��κ�һ���㶼�ƶ��������ƶ��ķ���;��붼��ͬ.
��ѡC.
C
�����������������ƽ�Ƶ�ʱ��ͼ���ϵ��κ�һ���㶼�ƶ��������ƶ��ķ���;��붼��ͬ.
��ѡC. ����ѡ���У���������֤�����⡰��a2��1����a��1���Ǽ�����ķ����ǣ�������
A. a=��2 B. a=��1 C. a=1 D. a=2
 A
�����������������������Ҫ���������þ�����֤��һ���������Ҫ˵����ѧ����Ĵ���ֻ��ٳ�һ����������������ѧ�г��õ�һ�ַ���������Ҫ֤��һ�����۲�����������ͨ���ٷ����ķ�����֤��һ�������Ǽ����⣮
����֤�����⡰��a2��1����a��1���Ǽ�����ķ��������ǣ�a=-2��
�ߣ�-2��2��1������a=-2��1��
��A��ȷ��
��ѡ��A��
A
�����������������������Ҫ���������þ�����֤��һ���������Ҫ˵����ѧ����Ĵ���ֻ��ٳ�һ����������������ѧ�г��õ�һ�ַ���������Ҫ֤��һ�����۲�����������ͨ���ٷ����ķ�����֤��һ�������Ǽ����⣮
����֤�����⡰��a2��1����a��1���Ǽ�����ķ��������ǣ�a=-2��
�ߣ�-2��2��1������a=-2��1��
��A��ȷ��
��ѡ��A�� 
