��Ŀ����
��ͼ��ʾ��DΪ��ABC�ı�AB���ӳ�����һ�㣬��D��DF��AC������ΪF����BC��E,��BD=BE,��֤����ABC�ǵ���������.
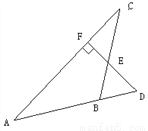
 ֤��������
������������������������Ʒ�����֤��ABC�ǵ��������Σ���ͼ��֪Ӧ֤AB=BC���ɡ��ȽǶԵȱߡ���Ӧ�뵽ֻҪ֤��A=��C���ɽǵĻ����ϵ��֪��A����D=90�㣬��C����CEF=90�㣬��CEF =��BED����BD=BE��֪��BED=��D���ɵá�A=��C�������֤��
�����������BD��BE�����BDE����BED��
�֡ߡ�BED����CEF�����BDE����CEF��
��...
֤��������
������������������������Ʒ�����֤��ABC�ǵ��������Σ���ͼ��֪Ӧ֤AB=BC���ɡ��ȽǶԵȱߡ���Ӧ�뵽ֻҪ֤��A=��C���ɽǵĻ����ϵ��֪��A����D=90�㣬��C����CEF=90�㣬��CEF =��BED����BD=BE��֪��BED=��D���ɵá�A=��C�������֤��
�����������BD��BE�����BDE����BED��
�֡ߡ�BED����CEF�����BDE����CEF��
��...
��ͼ������AΪֱ�Ƕ���ĵ���ֱ��������ABC��ֱ��BCƽ�Ƶõ���A��B��C�䣬ʹ��B����C�غϣ�����A��B����tan��A��BC�䣽________.

 ����������A������A��D��BC�䣬����ΪD��
�ڵ���ֱ��������A��B��C���У���A��D�ǵױ��ϵ����ߣ�
��B��C��=2 A��D��
��BC=B��C�䣬
��BD=BC+B��D=3 A��D��
�� tan��A��BC��=��
�ʴ�Ϊ�� .
����������A������A��D��BC�䣬����ΪD��
�ڵ���ֱ��������A��B��C���У���A��D�ǵױ��ϵ����ߣ�
��B��C��=2 A��D��
��BC=B��C�䣬
��BD=BC+B��D=3 A��D��
�� tan��A��BC��=��
�ʴ�Ϊ�� . һ�������������һ������ΪA������������ƽ��4����λ����ʱ��λ�ü�ΪB��������ƽ��3����λ����ʱ��λ�ü�ΪC������A��B��C��������ɵ������ε��ܳ�Ϊ ( )
A. 7 B. 14 C. 12 D. 15
 C
�������������������ͼ��ʾ��
AB��4��BC��3��
��AC��5��
����A��B��C��������ɵ������ε��ܳ�Ϊ��3��4��5��12��
��ѡC��
C
�������������������ͼ��ʾ��
AB��4��BC��3��
��AC��5��
����A��B��C��������ɵ������ε��ܳ�Ϊ��3��4��5��12��
��ѡC�� ��ͼ��ʾ��H�ǡ�ABC�ĸ�AD��BE�Ľ��㣬��DH=DC�������н��ۣ���BD=AD����BC=AC����BH=AC����CE=CD����ȷ���У�������
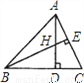
A. 1�� B. 2�� C. 3�� D. 4��
 B
����������������
�١�BE��AC��AD��BC�����AEH=��ADB=90�㣮
�ߡ�HBD+��BHD=90�㣬��EAH+��AHE=90�㣬��BHD=��AHE�����HBD=��EAH��
��DH=DC�����BDH�ա�ADC��AAS������BD=AD��BH=AC��
�ڡ�BC=AC�����BAC=��ABC��
�ɢ�֪����Rt��ABD�У���BD=AD�����ABC=45�㣬���BAC...
B
����������������
�١�BE��AC��AD��BC�����AEH=��ADB=90�㣮
�ߡ�HBD+��BHD=90�㣬��EAH+��AHE=90�㣬��BHD=��AHE�����HBD=��EAH��
��DH=DC�����BDH�ա�ADC��AAS������BD=AD��BH=AC��
�ڡ�BC=AC�����BAC=��ABC��
�ɢ�֪����Rt��ABD�У���BD=AD�����ABC=45�㣬���BAC... ��ͼ��һ������ֽƬ����ȥ���ֺ�õ�һ�������Σ���ͼ�С�1+��2�Ķ����ǣ� ��
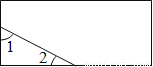
A. 30�� B. 60�� C. 90�� D. 120��
 C
�����������������������ã�ʣ�µ���������ֱ�������Σ�
���ԣ���1+��2=90�㣮
��ѡC��
C
�����������������������ã�ʣ�µ���������ֱ�������Σ�
���ԣ���1+��2=90�㣮
��ѡC�� �÷�֤��֤�����⡰��������������һ���ڽǴ��ڻ����60�㡱����һ��Ӧ���� ��
 �����ε������ڽǶ�С��60�㣮
��������
�����������Ƿ�֤���IJ��裬ֱ����ռ��ɣ�
�����������һ��Ӧ������۲��������������ε������ڽǶ�С��60�㣮
�����ε������ڽǶ�С��60�㣮
��������
�����������Ƿ�֤���IJ��裬ֱ����ռ��ɣ�
�����������һ��Ӧ������۲��������������ε������ڽǶ�С��60�㣮 ͼ��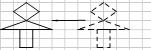 ��ߵ�ͼ�������ұߵ�ͼ������ƽ�Ƶõ��ģ�
��ߵ�ͼ�������ұߵ�ͼ������ƽ�Ƶõ��ģ�
 ����ƽ��6����λ.
���������������:�۲�ͼ���ж�Ӧ��ı仯�����ɵó�ͼ�εı仯����.
���������
����������Եõ���ߵ�ͼ�������ұߵ�ͼ������ƽ��6����λ����ƽ�Ƶõ���.
����ƽ��6����λ.
���������������:�۲�ͼ���ж�Ӧ��ı仯�����ɵó�ͼ�εı仯����.
���������
����������Եõ���ߵ�ͼ�������ұߵ�ͼ������ƽ��6����λ����ƽ�Ƶõ���. ����ͼ�ξ���ƽ�ƺ�ǡ�ÿ�����ԭͼ����ϳ�һ�������ε��ǣ� ��
A. ������ B. ������ C. ���� D. �����
 B
������������������������ܹ�ͨ��ƽ�ƶ��õ�����ͼ�κ�ԭͼ����ϳ�һ��������.
��ѡB.
B
������������������������ܹ�ͨ��ƽ�ƶ��õ�����ͼ�κ�ԭͼ����ϳ�һ��������.
��ѡB. �������ⲻ��ȷ���ǣ�������
A. �����ڽǷֱ���50���65����������ǵ���������
B. ���������ȵ��������ǵ���������
C. һ����ǵ�ƽ����ƽ����һ�ߵ��������ǵ���������
D. �����ڽDz���ȵ������β��ǵ���������
 D
���������⣺A����������180�㩁50�㩁65��=65�㣬��������ȵ��������ǵ��������Σ���ȷ��
B�������ȣ����Ӧ���ڽ�Ҳ��ȣ���������ȵ��������ǵ��������Σ���ȷ��
C��������ֱ��ƽ�У��ڴ�����ȣ�ͬλ��ȣ���֪����������ڽ�Ҳ��ȣ���������ȵ��������ǵ��������Σ���ȷ��
D�������ڽDz���ȵ������ο����ǵ��������Σ�����
��ѡD��
D
���������⣺A����������180�㩁50�㩁65��=65�㣬��������ȵ��������ǵ��������Σ���ȷ��
B�������ȣ����Ӧ���ڽ�Ҳ��ȣ���������ȵ��������ǵ��������Σ���ȷ��
C��������ֱ��ƽ�У��ڴ�����ȣ�ͬλ��ȣ���֪����������ڽ�Ҳ��ȣ���������ȵ��������ǵ��������Σ���ȷ��
D�������ڽDz���ȵ������ο����ǵ��������Σ�����
��ѡD�� 
