题目内容
如图所示,AB⊥BD,AC⊥CD,∠D=35°,则∠A的度数为( )
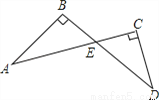
A. 65° B. 35° C. 55° D. 45°
 B
【解析】【解析】
∵AB⊥BD,AC⊥CD,∴∠B=∠C=90°,∴∠A+∠AEB=∠D+∠CED=90°.
又∵∠AEB=∠CED,∴∠A=∠D=35°.故选B.
B
【解析】【解析】
∵AB⊥BD,AC⊥CD,∴∠B=∠C=90°,∴∠A+∠AEB=∠D+∠CED=90°.
又∵∠AEB=∠CED,∴∠A=∠D=35°.故选B.
练习册系列答案
相关题目
下列属于分式方程的是( )
A. 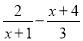 B.
B. 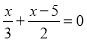
C. 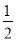 (x-1)=
(x-1)=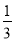 x D.
x D. 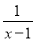 -x=1
-x=1
 D
【解析】试题解析:A,不是等式,所以不是方程,故不是分式方程.
B,C是一元一次方程,不是分式方程.
D.是分式方程.
故选D.
D
【解析】试题解析:A,不是等式,所以不是方程,故不是分式方程.
B,C是一元一次方程,不是分式方程.
D.是分式方程.
故选D. 如图,这是由一个边长为a的正方形沿一条对角线的方向平移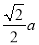 得到的图形,
得到的图形,
① 数一数这个图案中共有几个正方形;
② 若按此方法连续做4次平移,可得怎样的图案?该图案中共有几个正方形?

 3;15
【解析】试题分析:(1)根据正方形的定义即可得到答案.
(2)按此方法连续作4次平移画出图形,即可知道答案.
试题解析:
【解析】
(1)图中有3个正方形.
(2)图象如图所示,一共有15个正方形.
3;15
【解析】试题分析:(1)根据正方形的定义即可得到答案.
(2)按此方法连续作4次平移画出图形,即可知道答案.
试题解析:
【解析】
(1)图中有3个正方形.
(2)图象如图所示,一共有15个正方形. 在△ABC中,高AD和BE交于H点,且BH=AC,则∠ABC=______.
 45°或135°
【解析】【解析】
有2种情况.
(1)如图(1).
∵∠BHD=∠AHE,又∠AEH=∠ADC=90°,∴∠DAC+∠C=90°,∠HAE+∠AHE=90°,
∴∠AHE=∠C,∴∠C=∠BHD.
∵BH=AC,∠HBD=∠DAC,∠C=∠BHD,∴△HBD≌△CAD,∴AD=BD.
∴∠ABC=45°;
(2)如图(2).由(1)的解...
45°或135°
【解析】【解析】
有2种情况.
(1)如图(1).
∵∠BHD=∠AHE,又∠AEH=∠ADC=90°,∴∠DAC+∠C=90°,∠HAE+∠AHE=90°,
∴∠AHE=∠C,∴∠C=∠BHD.
∵BH=AC,∠HBD=∠DAC,∠C=∠BHD,∴△HBD≌△CAD,∴AD=BD.
∴∠ABC=45°;
(2)如图(2).由(1)的解... 如图,在△ABC中,∠C=60°,∠B=50°,D是BC上一点,DE⊥AB于点E,DF⊥AC于点F,则∠EDF的度数为( )
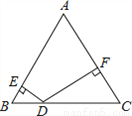
A. 90° B. 100° C. 110° D. 120°
 C
【解析】【解析】
在△ABC中,∵∠C=60°,∠B=50°,∴∠A=70°.
∵DE⊥AB于点E,DF⊥AC于点F,∴∠AED=∠AFD=90°,∴∠EDF=360°﹣∠A﹣∠AED﹣∠AFD=110°.故选C.
C
【解析】【解析】
在△ABC中,∵∠C=60°,∠B=50°,∴∠A=70°.
∵DE⊥AB于点E,DF⊥AC于点F,∴∠AED=∠AFD=90°,∴∠EDF=360°﹣∠A﹣∠AED﹣∠AFD=110°.故选C. Rt△ABC中,∠C=90°,∠B=46°,则∠A=( )
A. 44° B. 34° C. 54° D. 64°
 A
【解析】【解析】
∵∠C=90°,∠B=46°,∴∠A=90°﹣46°=44°.故选A.
A
【解析】【解析】
∵∠C=90°,∠B=46°,∴∠A=90°﹣46°=44°.故选A. 如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.
求证:(1)△ABC≌△ADC;(2)BO=DO.
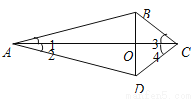
 (1)、证明过程见解析;(2)、证明过程见解析
【解析】试题分析:(1)、根据∠1=∠2,AC=AC,∠3=∠4得到△ABC和△ADC全等;(2)、根据全等得出AB=AD,然后结合∠1=∠2,AO=AO得出△ABO和△ADO全等,从而得到BO=DO.
试题解析:(1)、在△ABC和△ADC中∴△ABC≌△ADC.
(2)、∵△ABC≌△ADC ∴AB=AD 在△ABO和△ADO中...
(1)、证明过程见解析;(2)、证明过程见解析
【解析】试题分析:(1)、根据∠1=∠2,AC=AC,∠3=∠4得到△ABC和△ADC全等;(2)、根据全等得出AB=AD,然后结合∠1=∠2,AO=AO得出△ABO和△ADO全等,从而得到BO=DO.
试题解析:(1)、在△ABC和△ADC中∴△ABC≌△ADC.
(2)、∵△ABC≌△ADC ∴AB=AD 在△ABO和△ADO中... 平移只会改变图形的__________
 位置
【解析】试题解析:因为图形的平移前后,发生改变的是图形的位置.
故答案为:位置.
位置
【解析】试题解析:因为图形的平移前后,发生改变的是图形的位置.
故答案为:位置. 证明题:如图所示,在△ABC中,AB=AC,∠APB≠∠APC,求证:PB≠PC.
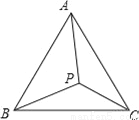
 证明见解析.
【解析】试题分析:运用反证法进行求解.
试题解析:证明:假设PB≠PC不成立,则PB=PC.
在△ABP和△ACP中,∵AB=AC,AP=AP,BP=CP,∴△ABP≌△ACP,∴∠APB=∠APC.
与∠APB≠∠APC相矛盾.因而PB=PC不成立,则PB≠PC.
证明见解析.
【解析】试题分析:运用反证法进行求解.
试题解析:证明:假设PB≠PC不成立,则PB=PC.
在△ABP和△ACP中,∵AB=AC,AP=AP,BP=CP,∴△ABP≌△ACP,∴∠APB=∠APC.
与∠APB≠∠APC相矛盾.因而PB=PC不成立,则PB≠PC. 
