题目内容
Rt△ABC中，∠C=90°，∠B=46°，则∠A=（ ）
A. 44° B. 34° C. 54° D. 64°
A
【解析】【解析】
∵∠C=90°，∠B=46°，∴∠A=90°﹣46°=44°．故选A．
举一反三期末百分冲刺卷系列答案计算：
(1) 
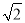(2cos 45°－sin 60°)＋
；
(2)sin 60°·cos 60°－tan 30°·tan 60°＋sin245°＋cos245°.
（1）2；（2）
【解析】试题分析：（1）先将特殊角的三角函数值代入，对最后一项的二次根式进行化简，然后再按运算顺序进行计算即可；
（2）将特殊角的三角函数值代入，按运算顺序进行计算即可得.
试题解析：（1）原式＝＝2；
（2）原式＝. 如图所示，△EFG是由△ABC沿水平方向平移得到的，如果∠ABC＝90°，AB=3 cm，BC＝2 cm，则EF＝_________，FG=_________，EG＝_________．
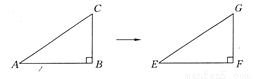
3 cm 2 cm cm
【解析】试题分析：在Rt△ABC中，AC＝＝＝（cm），
∵△EFG是由△ABC沿水平方向平移得到的，
∴EF＝AB＝3cm，FG＝BC＝2cm，EG＝AC＝cm．
故答案为3cm，2cm， cm． 下列说法错误的是（ ）
A. 直角三角板的两个锐角互余
B. 经过直线外一点只能画一条直线与已知直线平行
C. 如果两个角互补，那么，这两个角一定都是直角
D. 平行于同一条直线的两条直线平行
C
【解析】解：A．直角三角形中的两个锐角互余，所以直角三角板的两个锐角互余，故本选项说法正确；
B．根据平行公理可知：过直线外一点作已知直线的平行线，能作且只能作一条，故本选项说法正确；
C．如果两个角互补，那么，这两个角和一定是180°，但是它们不一定都是直角，故本选项说法错误；
D．根据平行线的传递性知平行于同一条直线的两条直线平行．故本选项说法正确．
故选C．... 如图所示，AB⊥BD，AC⊥CD，∠D=35°，则∠A的度数为（ ）
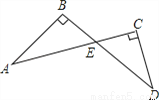
A. 65° B. 35° C. 55° D. 45°
B
【解析】【解析】
∵AB⊥BD，AC⊥CD，∴∠B=∠C=90°，∴∠A+∠AEB=∠D+∠CED=90°．
又∵∠AEB=∠CED，∴∠A=∠D=35°．故选B． 四边形ABCD是正方形．
(1)如图(1)所示，点G是BC边上任意一点(不与B，C两点重合)，连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证△ABF≌△DAE；
(2)在(1)中，线段EF与AF，BF的等量关系是____；(不需证明，直接写出结论即可)
(3)如图(2)所示，若点G是CD边上任意一点(不与C，D两点重合)，作BF⊥AG于点F，DE⊥AG于点E，那么图中的全等三角形是____，线段EF与AF，BF的等量关系是____．(不需证明，直接写出结论即可)
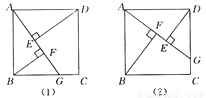
EF＝AF－BF △ABF≌△DAE EF＝BF－AF
【解析】试题分析：（1）根据正方形的性质可知：△ABF≌△ADE；
（2）利用全等三角形的性质，AE=BF，AF=DE，得出AF-BF=EF；
（3）同理可得出图（2），△ABF≌△DAE，EF=BF-AF．
(1) 证明：在正方形ABCD中，AB＝AD，∠BAD＝90°，
∴∠BAF+∠DAE＝90°．
... 在等腰梯形ABCD中，∠ABC＝2∠ACB，BD平分∠ABC，AD∥BC，如图所示，则图中的等腰三角形有( )
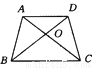
A. 1个 B. 2个 C. 3个 D. 4个
D
【解析】∵AD∥BC，∠ADB=30°，
∴∠CBD=∠ADB=30°.
∵ABCD为等腰梯形，
∴∠ABC=∠DCB=60°，则∠BAD=∠ABC-∠CBD=30°，
∴△ABD为等腰三角形.
同理可证△ACD为等腰三角形，
∵∠ABO=∠DCO=30°，∠AOB=∠DOC，AB=CD，
∴△AOB≌△DOC，
∴AO=DO，BO=CO，... 平移前后两个图形是图形，对应点连线（ ）
A. 平行但不相等
B. 不平行也不相等
C. 平行且相等
D. 不相等
C
【解析】试题解析：平移前后两个图形是全等图形，对应点连线平行且相等.
故选C. 如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（ ）
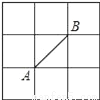
A. 6 B. 7 C. 8 D. 9
C
【解析】试题分析：如图：分情况讨论
①AB为等腰△ABC底边时，符合条件的C点有2个；
②AB为等腰△ABC其中的一条腰时，符合条件的C点有4个．
故选A．