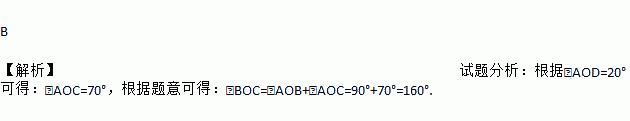题目内容
将一副直角三角尺如图放置，若∠AOD=20°， 则∠BOC的大小为（ ）
A. 140° B. 160° C. 170° D. 150°
B
【解析】试题分析：根据∠AOD=20°可得：∠AOC=70°，根据题意可得：∠BOC=∠AOB+∠AOC=90°+70°=160°.
活力课时同步练习册系列答案一次函数的图象经过点(tan 45°，tan 60°)和(－cos 60°，－6tan 30°)，则此一次函数的表达式为________．
y＝2x－
【解析】tan 45°＝1，tan 60°＝，－cos 60°＝－，－6tan 30°＝－2，
设y＝kx＋b的图象经过点(1， )，（－ ，-2），
则有，解得： ，
∴一次函数解析式为： ，
故答案为： . 下列现象：(1)电风扇的转动；(2)打气筒打气时，活塞的运动；(3)钟摆的摆动；(4)传送带上瓶装饮料的移动．其中属于平移的是_________．
(2)(4)
【解析】试题分析：（1）电风扇的转动是旋转，不属于平移；
（2）打气筒打气时，活塞的运动属于平移；
（3）钟摆的摆动是旋转，不属于平移；
（4）传送带上瓶装饮料的移动符合平移的性质，属于平移．
故选D． 已知，如图，△ABC中，∠BAC=90°，AD⊥BC于D，则图中相等的锐角的对数有（ ）
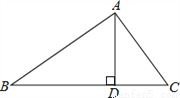
A. 4对 B. 3对 C. 2对 D. 1对
C
【解析】【解析】
相等的锐角有：∠B=∠CAD，∠C=∠BAD共2对．故选C． 如图，O是∠BAC内一点，且点O到AB，AC的距离OE=OF，则△AEO≌△AFO的依据是（ ）
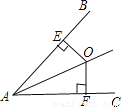
A.HL B.AAS C.SSS D.ASA
A
【解析】
试题分析：利用点O到AB，AC的距离OE=OF，可知△AEO和△AFO是直角三角形，然后可直接利用HL求证△AEO≌△AFO，即可得出答案．
【解析】
∵OE⊥AB，OF⊥AC，∴∠AEO=∠AFO=90°，
又∵OE=OF，AO为公共边，∴△AEO≌△AFO．
故选A． 文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时，画出图形，写出“已知”，“求证”（如图），她们对各自所作的辅助线描述如下：
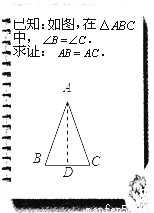
文文：“过点A作BC的中垂线AD，垂足为D”；
彬彬：“作△ABC的角平分线AD”．
数学老师看了两位同学的辅助线作法后，说：“彬彬的作法是正确的，而文文的作法需要订正．”
（1）请你简要说明文文的辅助线作法错在哪里；
（2）根据彬彬的辅助线作法，完成证明过程．
（1）作辅助线不能同时满足两个条件；（2）证明见解析.
【解析】试题分析：（1）线段BC的中垂线可以直接作出的，不需要附带“过点A作”；
（2）根据已知条件利用AAS可证△ABD≌△ACD，得出AB=AC．
试题解析：（1）作辅助线不能同时满足两个条件；
（2）证明：作△ABC的角平分线AD．
∴∠BAD=∠CAD，
在△ABD与△ACD中，
∴△ABD≌... 如图所示，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD，则∠A等于( )
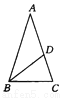
A. 30° B. 40° C. 45° D. 36°
D
【解析】∵AD＝BD，
∴∠A＝∠ABD，
∴∠BDC＝2∠A.
∵BD＝BC，
∴∠C＝∠BDC＝2∠A．
∵AB＝AC，
∴∠ABC＝∠C＝2∠A，
由三角形内角和定理，得∠A+2∠A+2∠A＝180°，
即∠A＝36°．
故选D. 平移前后的两个图形相互比较而言，下列说法正确的是（ ）
A. 两个图形大小不一样
B. 两个图形的形状不一样
C. 平移前比平移后小
D. 两个图形全等
D
【解析】试题解析：平移不改变图形的大小和形状,平移前后的两个图形全等.
故选D. 如图，在△ABC中，AB=AC，E是AB的中点，以点E为圆心，EB为半径画弧，交BC于点D，连接ED并延长到点F，使DF=DE，连接FC，若∠B=70°，则∠F的度数是（ ）
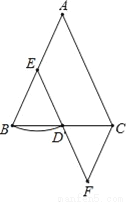
A. 40 B. 70 C. 50 D. 45
A
【解析】【解析】
∵以点E为圆心，EB为半径画弧，交BC于点D，∴EB=ED，∴∠EDB=∠B=70°，∴∠BED=180°﹣∠B=∠BDE=40°．
∵AB=AC，∴∠ACB=∠B，∴∠EDB=∠ACB，∴EF∥AC．
∵E是AB的中点，即BE=AE，∴BD=CD．
在△EBD和△FCD中，∵DE=DF，∠EDB=∠CDF，BD=CD，∴△EBD≌△FCD（SAS）...