题目内容
如图，一个矩形纸片，剪去部分后得到一个三角形，则图中∠1+∠2的度数是（ ）
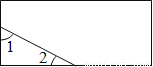
A. 30° B. 60° C. 90° D. 120°
C
【解析】试题分析：由题意得，剩下的三角形是直角三角形，
所以，∠1+∠2=90°．
故选C．
练习册系列答案
相关题目
在△ABC中，∠C＝90°，∠A，∠B，∠C所对的边分别为a，b，c.
(1)已知c＝8
，∠A＝60°，求∠B，a，b；
(2)已知a＝3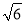
，∠A＝45°，求∠B，b，c.
(1)∠B＝30°，a＝12，b＝4；(2)∠B＝45°，b＝3，c＝6.
【解析】试题分析：（1）根据直角三角形两锐角互余求得∠B的度数，再根据30度角所对直角边等于斜边一半求得b，再根据勾股定理求得a即可；
（2）先根据直角三角形两锐角互余求得∠B=45°，从而得到b=a，再利用勾股定理即可求得c.
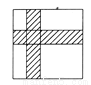
试题解析：（1）∵∠C=90°，∠A=60°，∴∠B=90°-∠A=30°，... 如图所示，一张白色正方形纸片的边长是10 cm，被两张宽为2 cm的阴影纸条分为四个白色的长方形部分，请你利用平移的知识求出图中白色部分的面积．
64 cm2
【解析】试题分析：将横向的小路平移至正方形的上边，将纵向小路平移至正方形的左边，则剩余部分即为白色部分的面积．
【解析】
将横向的小路平移至正方形的上边，将纵向小路平移至正方形的左边，
所以白色部分的面积＝(10－2)(10－2)＝64cm2． 如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：_____________，使△AEH≌△CEB．
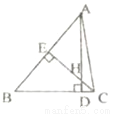
AH＝BC或EA＝EC或EH＝EB等；
【解析】∵AD⊥BC，CE⊥AB，垂足分别为D、E，
∴∠BEC=∠AEC=90°，
在Rt△AEH中，∠EAH=90°﹣∠AHE，
又∵∠EAH=∠BAD，
∴∠BAD=90°﹣∠AHE，
在Rt△AEH和Rt△CDH中，∠CHD=∠AHE，
∴∠EAH=∠DCH，
∴∠EAH=90°﹣∠CHD=∠BCE，
... 在直角三角形中，其中一个锐角是另一个锐角的2倍，则此三角形中最小的角是（ ）
A. 15° B. 30° C. 60° D. 90°
B
【解析】【解析】
设较小的锐角是x°，则另一个锐角是2x°．
由题意得：x+2x=90，解得x=30．
即此三角形中最小的角是30°．
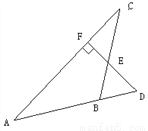
故选B． 如图所示，D为△ABC的边AB的延长线上一点，过D作DF⊥AC，垂足为F，交BC于E,且BD=BE,求证：△ABC是等腰三角形.
证明见解析
【解析】试题分析：可用逆推法，欲证△ABC是等腰三角形，由图可知应证AB=BC，由“等角对等边”，应想到只要证∠A=∠C．由角的互余关系可知∠A＋∠D=90°，∠C＋∠CEF=90°，∠CEF =∠BED，由BD=BE可知∠BED=∠D，可得∠A=∠C，本题得证．
试题解析：∵BD＝BE，∴∠BDE＝∠BED，
又∵∠BED＝∠CEF，∴∠BDE＝∠CEF，
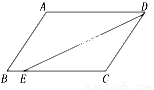
又... 如图，在□ABCD中，已知AD=8cm，AB=6cm，DE平分∠ADC交BC边于点E，则BE等于（ ）
A. 2cm B. 4cm C. 6cm D. 8cm
A
【解析】试题分析：由平行四边形对边平行根据两直线平行，内错角相等可得∠EDA=∠DEC，而DE平分∠ADC，进一步推出∠EDC=∠DEC，在同一三角形中，根据等角对等边得CE=CD=6，则BE可求BE=BC-EC=8-6=2．
故选：A． 经过平移，________________和________________平行且相等
对应点所连的线段 对应线段
【解析】试题解析：平移前后对应点所连的线段和对应线段平行且相等.
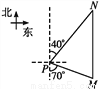
故答案为：(1). 对应点所连的线段 (2). 对应线段. 如图,一艘海轮位于灯塔P南偏东70°方向的M处,它以每时40海里的速度向正北方向航行,2时后到达位于灯塔P北偏东40°方向的N处,则N处与灯塔P的距离为( )
A. 40海里 B. 60海里
C. 70海里 D. 80海里
D
【解析】试题解析：MN=2×40=80（海里），
∵∠M=70°，∠N=40°，
∴∠NPM=180°-∠M-∠N=180°-70°-40°=70°，
∴∠NPM=∠M，
∴NP=MN=80（海里）．
故选D．