题目内容
下列说法中不正确的是（ ）
A. 平行四边形是中心对称图形
B. 斜边及一锐角分别相等的两直角三角形全等
C. 两个锐角分别相等的两直角三角形全等
D. 一直角边及斜边分别相等的两直角三角形全等
C
【解析】解：A．平行四边形是中心对称图形，说法正确；
B．斜边及一锐角分别相等的两直角三角形全等，说法正确；
C．两个锐角分别相等的两直角三角形全等，说法错误；
D．一直角边及斜边分别相等的两直角三角形全等，说法正确．
故选C．
练习册系列答案
相关题目
如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D′处，那么tan∠BAD′＝________.
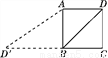
【解析】由题知，∠ABD′=90°，BD=BD′==2，，
∴tan∠BAD′==，
故答案为： . 如图所示，△ABC经过平移得到△DEF，已知CE＝2 cm，AC＝3 cm，AB＝4 cm，∠A＝90°，则CF＝_________cm，平移的距离是_________．
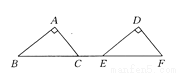
7 7 cm
【解析】试题分析：在Rt△ABC中，由勾股定理得：
BC＝＝＝5（cm），
∵△ABC经过平移得到△DEF，
∴EF＝BC＝5cm，
∴CF＝CE＋EF＝2＋5＝7（cm），
∵C点与F点对应，
∴平移的距离是CF的长度，
即平移的距离是7cm．
故答案为：7，7cm． 如图，在△ABC中，∠C=60°，∠B=50°，D是BC上一点，DE⊥AB于点E，DF⊥AC于点F，则∠EDF的度数为（ ）
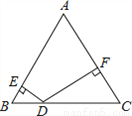
A. 90° B. 100° C. 110° D. 120°
C
【解析】【解析】
在△ABC中，∵∠C=60°，∠B=50°，∴∠A=70°．
∵DE⊥AB于点E，DF⊥AC于点F，∴∠AED=∠AFD=90°，∴∠EDF=360°﹣∠A﹣∠AED﹣∠AFD=110°．故选C． 下列可使两个直角三角形全等的条件是（ ）
A. 一条边对应相等 B. 两条直角边对应相等
C. 一个锐角对应相等 D. 两个锐角对应相等
B
【解析】【解析】
两直角三角形隐含一个条件是两直角相等，要判定两直角三角形全等，起码还要两个条件，故可排除A、C；
而D构成了AAA，不能判定全等；
B构成了SAS，可以判定两个直角三角形全等．
故选B． 如图，四边形ABCD的对角线AC与BD相交于O点，∠1=∠2，∠3=∠4．
求证：(1)△ABC≌△ADC；(2)BO=DO．
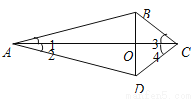
(1)、证明过程见解析；(2)、证明过程见解析
【解析】试题分析：(1)、根据∠1=∠2，AC=AC，∠3=∠4得到△ABC和△ADC全等；(2)、根据全等得出AB=AD，然后结合∠1=∠2，AO=AO得出△ABO和△ADO全等，从而得到BO=DO.
试题解析：(1)、在△ABC和△ADC中∴△ABC≌△ADC．
(2)、∵△ABC≌△ADC ∴AB=AD 在△ABO和△ADO中... 连续平移只改变图形的那方面，没有改变图形的哪几方面？
连续平移只改变图形的位置，没有改变图形的形状、大小.
【解析】试题分析：根据平移的特征回答即可.
试题解析：
根据平移的特征可以得出连续平移只改变图形的位置，没有改变图形的 形状、大小. 下列说法正确的是( )
A. 平移改变图形的形状
B. 平移改变图形的大小
C. 平移改变物体的形状和大小
D. 平移不改变物体的形状和大小
D
【解析】试题解析：平移的特点是不变形，即平移不改变物体的形状和大小.
故选D. 用反证法证明“三角形中至少有一个内角不小于60°”，应先假设这个三角形中（ ）
A. 有一个内角小于60° B. 每一个内角都小于60°
C. 有一个内角大于60° D. 每一个内角都大于60°
B
【解析】试题分析：此题要运用反证法，由题意先假设三角形的三个角都小于60°成立．然后推出不成立．得出选项．
【解析】
设三角形的三个角分别为：a，b，c．
假设，a＜60°，b＜60°，c＜60°，
则a+b+c＜60°+60°+60°，
即，a+b+c＜180°与三角形内角和定理a+b+c=180°矛盾．
所以假设不成立，即三角形中至少有一个角不小于60...