题目内容
如图，O是∠BAC内一点，且点O到AB，AC的距离OE=OF，则△AEO≌△AFO的依据是（ ）
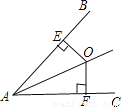
A.HL B.AAS C.SSS D.ASA
A
【解析】
试题分析：利用点O到AB，AC的距离OE=OF，可知△AEO和△AFO是直角三角形，然后可直接利用HL求证△AEO≌△AFO，即可得出答案．
【解析】
∵OE⊥AB，OF⊥AC，∴∠AEO=∠AFO=90°，
又∵OE=OF，AO为公共边，∴△AEO≌△AFO．
故选A．
小红家的阳台上放置了一个晒衣架(如图①)，图②是晒衣架的侧面示意图，立杆AB，CD相交于点O，B，D两点立于地面，经测量：AB＝CD＝136 cm，OA＝OC＝51 cm，OE＝OF＝34 cm，现将晒衣架完全稳固张开，扣链EF成一条线段，且EF＝32 cm(参考数据：sin 61.9°≈0.882，cos 61.9°≈0.471，tan 28.1°≈0.534)．
(1)求证：AC∥BD.
(2)求扣链EF与立杆AB的夹角∠OEF的度数(结果精确到0.1°)．
(3)小红的连衣裙穿在晒衣架上的总长度达到122 cm，垂挂在晒衣架上是否会拖落到地面？请通过计算说明理由．
（1）见解析；（2）61.9°；（3）会拖落到地面．
【解析】试题解析
（1）证明：证法一： 相交于点 ，
同理可证：
证法二：
∴
又
（2）【解析】
在中， 作于点，
则
用计算器求得
（3）解法一：小红的连衣裙会拖落到地面；
在中，
过点 作于点，
同可证：
则
∴所以：小红的连衣裙垂挂在衣架后的总... 如图所示，△ABC沿射线MN方向平移一定距离后成为△A′B′C′．找出两个三角形中平行且相等的线段以及全等的三角形．
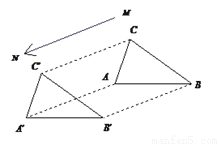
AB、A′B′；BC、B′C′；AC、A′C′；△ABC≌△A′B′C′
【解析】试题分析：根据平移前后两个图形的对应线段平行且相等可以直接找出两个三角形中平行且相等的线段；根据平移前后的两个图形全等可知直接找出全等的三角形．
试题解析：
【解析】
两个三角形中平行且相等的线段有：AB与A’B’，BC与B’C’，AC与A’C’；
全等的三角形是：△ABC≌△A’B’C’．... 在一个直角三角形中，有一个锐角等于30°，则另一个锐角的大小为______度．
60
【解析】【解析】
∵三角形是直角三角形，一个锐角等于30°，∴另一个锐角为90°﹣30°=60°．
故答案为：60． 如果两个直角三角形的两条直角边对应相等，那么这两个直角三角形全等的依据是（ ）
A. SSS B. AAS C. SAS D. HL
C
【解析】【解析】
两边及夹角对应相等的两个三角形全等，这为“边角边”定理，简写成“SAS”．故选C． 将一副直角三角尺如图放置，若∠AOD=20°， 则∠BOC的大小为（ ）
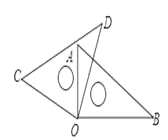
A. 140° B. 160° C. 170° D. 150°
B
【解析】试题分析：根据∠AOD=20°可得：∠AOC=70°，根据题意可得：∠BOC=∠AOB+∠AOC=90°+70°=160°. 等腰三角形的顶角α＞90°，如果过其顶角的顶点作一条直线将这个等腰三角形分 成了两个等腰三角形，那么α的度数为________．
108°
【解析】如图，
∵AB=AC，BD=AD，AC=CD，
∴∠1=∠B，∠2=∠4，∠B=∠C，
∵∠4=∠1+∠B=2∠B=2∠C，
∴∠2=∠4=2∠C，
∵∠2+∠4+∠C=180°，
∴5∠C=180°，
∴∠C=36°，
∴α=∠BAC=180°-2∠C=108°． 平移不改变图形的 ___________和 ___________
形状 大小
【解析】试题解析：平移不改变图形的形状和大小.
故答案为：(1). 形状 (2). 大小. 如图，AD是△ABC的边BC上的高，由下列条件中的某一个就能推出△ABC是等腰三角形的是__．
①∠BAD=∠ACD；②∠BAD=∠CAD；③AB+BD=AC+CD；④AB﹣BD=AC﹣CD．
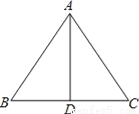
②③④
【解析】【解析】
应添加的条件是②③④；
证明：②当∠BAD=∠CAD时，∵AD是∠BAC的平分线，且AD是BC边上的高，则△ABD≌△ACD，∴△BAC是等腰三角形；
③延长DB至E，使BE=AB；延长DC至F，使CF=AC；连接AE、AF．
∵AB+BD=CD+AC，∴DE=DF，又AD⊥BC，∴△AEF是等腰三角形，∴∠E=∠F．
∵AB=BE，∴∠A...