如图，在△ABC中，AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，M为AD上任意一点，则下列结论中错误的是( )
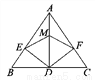
A. DE＝DF B. ME＝MF
C. AE＝AF D. BD＝CD
D
【解析】∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴∠BAD=∠CAD，∠AED=∠AFD=90°，
又∵AD=AD，
∴△ADE≌△ADF，
∴DE=DF，AE=AF，
∵AE=AF，∠BAD=∠CAD，AM=AM，
∴△AME≌△AMF，
∴ME=MF，
故选项A、B、C正确，
无法得到BD=CD，故选项D错误，
故选D... 如图所示，四边形ABCD中，AE、AF分别是BC、CD的垂直平分线，∠EAF＝80°，∠CBD＝30°，则∠ADC的度数为( )
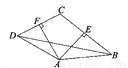
A. 45° B. 60°
C. 80° D. 100°
B
【解析】连接AC，
∵AE、AF分别是BC、CD的垂直平分线，
∴AB=AC=AD，
∵AF⊥DC，AE⊥BC，
∴∠CAF=∠DAF，∠CAE=∠BAE．
∴∠DAB=2∠EAF=160°，
∴∠ABD=（180°-160°）÷2=10°，
∴∠ABC=∠ACB=30°+10°=40°；
在四边形AECF中，
∠FCE=360°-9... 如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC、CD上分别找一个点M、N，使△AMN周长最小时，∠AMN＋∠ANM的度数为( )
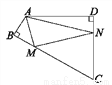
A. 130° B. 120°
C. 110° D. 100°
B
【解析】作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值，作DA延长线AH，
∵∠DAB=120°，
∴∠HAA′=60°，
∴∠AA′M+∠A″=∠HAA′=60°，
∵∠MA′A=∠MAA′，∠NAD=∠A″，
且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，
∴∠AMN... 在△ABC中，AB=AC，若∠A=40°，则∠B=__________度.
70
【解析】∵AB=AC，
∴∠B=∠C，
∵∠A=40°，
∴∠B=∠C=(180?40)=70°，
故答案为：70. 在“线段、锐角、三角形、等边三角形”这四个图形中，其中是轴对称图形的有___个，其中对称轴最多的是__________.
3 等边三角形
【解析】线段有两条对称轴，锐角有一条对称轴，等边三角形有三条对称轴，
故答案为：3，等边三角形． 小明衣服上的号码在镜子中如图，则小明衣服上的实际号码是___.
25
【解析】∵照镜子时，图中的数字与实际数字成轴对称，
∴小明衣服上的实际号码为25，
故答案为：25． 如图，BC＝32cm，DE是AB的垂直平分线，D是垂足，DE交BC于E，AC＝18cm，则△AEC的周长为___cm.
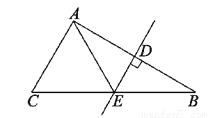
50
【解析】∵DE是AB的垂直平分线，
∴AE=BE．
∴△AEC的周长=AC+CE+AE=AC+BC=18+32=50（cm），
故答案为：50． 等腰三角形一腰上的中线将它的周长分别为8和12两部分，则它的腰长、底边长分别为__________________.
8,8,4或
【解析】设底边长a,腰长b,则有
（1）a+=8，
b+=12，
解得：a=4，b=8，
即腰长、底边长分别为：8，8，4；
（2）a+=12，
b+=8，
得a= ，b=，
即腰长、底边长分别为： ， ， ，
综上，腰长、底边长分别为：8，8，4或， ， ，
故答案为：8，8，4或， ， . 已知等腰△ABC中，AB=AC，D是BC边上一点，连接AD，若△ACD和△ABD都是等腰三角形，则∠C的度数是 ．
36°或45°．
【解析】
试题分析：△ACD和△ABD都是等腰三角形，但没有说具体的边相等，所以应分情况讨论．
（1）AD=BD，DC=AD，那么△ADB和△ADC是全等三角形，可求得∠ADC=90°，那么∠C=45°；
（2）AB=BD，CD=AD，那么∠B=∠C=∠DAC，∠BAD=∠BDA=2∠C，然后用∠C表示出△ABC的内角和，即可求得5∠C=180°，那么∠C... 如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=______。
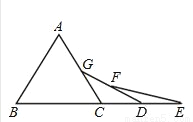
15°
【解析】试题分析：设∠E=x，根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
【解析】
设∠E=x，
∵DF=DE，
∴∠DFE=∠E=x，
∴∠CDG=∠E+∠DFE=2x，
∵CG=CD，
∴∠CDG=∠CGD=2x，
∴∠ACB=∠CDG+∠CGD=2x+2x=4x，
∵∠ACB=70°，...