题目内容
在△ABC中，AB=AC，若∠A=40°，则∠B=__________度.
70
【解析】∵AB=AC，
∴∠B=∠C，
∵∠A=40°，
∴∠B=∠C=(180?40)=70°，
故答案为：70.
练习册系列答案
阅读快车系列答案
相关题目
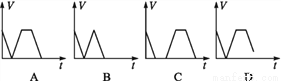
有一游泳池注满水,现按一定速度将水排尽,然后进行清洗,再按相同速度注满清水,使用一段时间后,又按相同的速度将水排尽,则游泳池的存水量V(m3)随时间t(h)变化的大致图象是( )
C
【解析】【解析】
根据题意分析可得：存水量V的变化有几个阶段：
1、减小为0，并持续一段时间；
2、增加至最大，并持续一段时间；
3、减小为0．
故选A． 如果m＜n＜0，那么下列结论中错误的是（ ）
A、m－9＜n－9 B、－m＞－n C、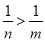
D、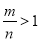
C
【解析】
试题分析：根据不等式的基本性质依次分析各项即可.
m＜n＜0，
∴m－9＜n－9，－m＞－n，，，
故选C. 如图，在等边△ABC中，P为△ABC内任意一点，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，AM⊥BC于M，试猜想AM、PD、PE、PF之间的关系，并说明你的猜想．
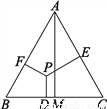
AM＝PD＋PE＋PF，理由见解析
【解析】试题分析：连接AP、BP、CP，根据面积相等，又利用△ABC是等边三角形，即可得PE+PD+PF=AM.
试题解析：PE+PD+PF=AM，理轴如下：
连接AP、BP、CP，
∵S△ABP+S△BCP+S△ACP=S△ABC，
∴AB×PE+BC×PD+AC×PF＝BC×AM，
∵△ABC是等边三角形，
∴AB=... 已知等腰△ABC中，AB=AC，D是BC边上一点，连接AD，若△ACD和△ABD都是等腰三角形，则∠C的度数是 ．
36°或45°．
【解析】
试题分析：△ACD和△ABD都是等腰三角形，但没有说具体的边相等，所以应分情况讨论．
（1）AD=BD，DC=AD，那么△ADB和△ADC是全等三角形，可求得∠ADC=90°，那么∠C=45°；
（2）AB=BD，CD=AD，那么∠B=∠C=∠DAC，∠BAD=∠BDA=2∠C，然后用∠C表示出△ABC的内角和，即可求得5∠C=180°，那么∠C... 请你用所学的知识，在下面两项中任选其一作图．
（1）参考下图，为班级的黑板报设计一组花边图案．
（2）以三角形、矩形、圆形为“基本图案”通过平移、旋转、轴对称为班级设计一个班徽．
见解析
【解析】试题分析：本题主要考查大家根据轴对称性质设计花边图案的能力，而且要符合考题中的四点要求，这是一道融数学与美术为一体的综合创新素质题
试题解析：【解析】
选（1）．如图：设计花边图案为： 我国国旗上的四个小五角星，通过_______________移动可以相互得到．
旋转或旋转和平移
【解析】【解析】
四个小五角星通过旋转可以互相得到．故答案为：旋转． 某市为治理污水，需要铺设一段全长600m的污水排放管道，铺设120m后，为加快施工进度，后来每天比原计划增加20m，结果共用11天完成这一任务，求原计划每天铺设管道的长度．如果设原计划每天铺设xm管道，那么根据题意，可列方程 ．
．
【解析】
试题分析：由题意可得，，化简，得：，故答案为：． 把a2﹣4a多项式分解因式，结果正确的是（ ）
A. a（a﹣4） B. （a+2）（a﹣2） C. a（a+2）（a﹣2） D. （a﹣2）2﹣4
A
【解析】试题分析： a2-4a=a（a-4），
故选A．