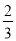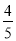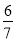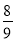题目内容
如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=______。
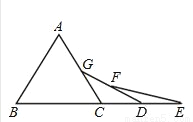
15°
【解析】试题分析：设∠E=x，根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
【解析】
设∠E=x，
∵DF=DE，
∴∠DFE=∠E=x，
∴∠CDG=∠E+∠DFE=2x，
∵CG=CD，
∴∠CDG=∠CGD=2x，
∴∠ACB=∠CDG+∠CGD=2x+2x=4x，
∵∠ACB=70°，...
练习册系列答案
相关题目
宁宁同学设计了一个计算程序如下表:
输入数据 | 1 | 2 | 3 | 4 | 5 | … |
输出数据 |
|
|
|
|
| … |
根据表格中的数据的对应关系,可得出输出数据y与输入数据x之间的关系式为_____.
y=
【解析】【解析】
根据题意，得： ．故答案为： ． 有下列说法：
（1）若a＜b，则－a＞－b； （2）若xy＜0，则x＜0，y＜0；
（3）若x＜0，y＜0，则xy＜0； （4）若a＜b，则2a＜a＋b；
（5）若a＜b，则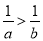
； （6）若
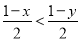，则x＞y.
其中正确的说法有（ ）
A、2个 B、3个 C、4个 D、5个
B
【解析】
试题分析：根据不等式的基本性质依次分析各项即可。
（1）若a＜b，则－a＞－b，正确；
（2）若xy＜0，则x＜0，y＞0或x＞0，y＜0，错误；
（3）若x＜0，y＜0，则xy＞0，错误；
（4）若a＜b，则2a＜a＋b，正确；
（5）若a＜0＜b，则，错误；
（6）若，则x＞y，正确.
故选B. 由下列条件不能判定△ABC是直角三角形的是( )
A. ∠A＝37°，∠C＝53° B. ∠A－∠C＝∠B
C. ∠A∶∠B∶∠C＝3∶4∶5 D. ∠A∶∠B∶∠C＝2∶3∶5
C
【解析】解：A．∠B=180°－（37°+53°）=90°，是直角三角形；
B．∠B+∠C=∠A=180°－∠A，∴∠A=90°，是直角三角形；
C．∠C=180°×=75°，不是直角三角形；
D．∠C=180°×=90°，是直角三角形．
故选C． 如图，AD是△ABC的角平分线，DE⊥AB于E，DF⊥AC于F，直线AD交EF于点O.问直线AD是线段EF的垂直平分线吗？请说明理由．
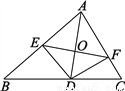
AD是线段EF的垂直平分线，理由见解析
【解析】试题分析：由AD为△ABC的角平分线，得到DE=DF，推出∠AEF和∠AFE相等，得到AE=AF，即可推出结论.
试题解析：∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE=DF，∠AED=∠AFD=90°，
∴∠DEF=∠DFE，
∴∠AEF=∠AFE，
∴AE=AF，
∴点A、D都在EF的垂直... 在“线段、锐角、三角形、等边三角形”这四个图形中，其中是轴对称图形的有___个，其中对称轴最多的是__________.
3 等边三角形
【解析】线段有两条对称轴，锐角有一条对称轴，等边三角形有三条对称轴，
故答案为：3，等边三角形． 请充分发挥你的想象力，任选其一完成下面的设计
（1）以一直角三角形为“基本图形”，利用旋转而得到一个风车或风轮图案．你能设计出几种风车风轮图案呢？请将你的图案画出来，完成后与同学进行交流．
（2）利用圆、三角形、正六边形，通过平移或旋转来设计一个图案，完成后与同学交流你的作品，说明你的设计意图．
见解析
【解析】试题分析：根据旋转的角度不同可得到不同的风车形状，只要满足题意即可．
试题解析：【解析】
选（1），所画的是旋转90°的情况． 已知方程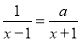
的解为x=2，求
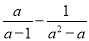的值．
， .
【解析】试题分析：根据分式方程的解为x=2，代入到分式方程，求出a的值，把通分化简，再把a的值代入计算即可求出代数式的值．
把x=2代入得，a=3，
∴原式=﹣
=
=，
当a=3时，原式==． 右图中四边形均为长方形，根据图形，写出一个正确的等式：_____________．
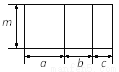
m（a+b+c）=ma+mb+mc（答案不唯一）．
【解析】试题分析：从两方面计算该图形的面积即可求出该等式
本题解析：从整体来计算矩形的面积：m(a+b+c)，
从部分来计算矩形的面积：ma+mb+mc，
所以m(a+b+c)=ma+mb+mc
故答案为：m(a+b+c)=ma+mb+mc