题目内容
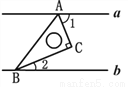
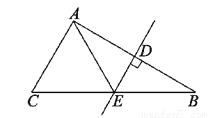
如图，BC＝32cm，DE是AB的垂直平分线，D是垂足，DE交BC于E，AC＝18cm，则△AEC的周长为___cm.
50
【解析】∵DE是AB的垂直平分线，
∴AE=BE．
∴△AEC的周长=AC+CE+AE=AC+BC=18+32=50（cm），
故答案为：50．
练习册系列答案
相关题目
如图，在△ABC中，按以下步骤作图：①分别以A、B为圆心，大于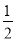
AB的长为半径画弧，相交于两点M，N；②作直线MN交AC于点D，连接BD．若∠A＝25°，则∠CDB＝（ ）
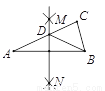
A. 25° B. 90° C. 50° D. 60°
C
【解析】试题解析：由作图的步骤可知，直线MN是线段AB的垂直平分线，
∴DA=DB，
∴∠DBA=∠A=25°，
∴∠CDB=∠DBA+∠A=50°，
故选C． 如果t＞0，那么a＋t与a的大小关系是（ ）
A、a＋t＞a B、a＋t＜a C、a＋t≥a D、不能确定
A
【解析】
试题分析：根据不等式的基本性质即可得到结果.
t＞0，
∴a＋t＞a，
故选A. 
如图，在正方形网格上有一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法)；
(2)在网格上的最小正方形的边长为1，求△ABC的面积．
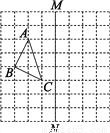
(1)见解析;（2）
【解析】试题分析：（1）根据网格特点分别找到A、B、C关于直线MN对称的点，然后顺次连接即可得；
（2）用三角形ABC所在长方形的面积减去四周三个小三角形的面积即可得.
试题解析：（1）如图所示：
（2）S△ABC＝2×3－2×(×1×2)－×1×3＝. 如图所示，四边形ABCD中，AE、AF分别是BC、CD的垂直平分线，∠EAF＝80°，∠CBD＝30°，则∠ADC的度数为( )
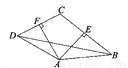
A. 45° B. 60°
C. 80° D. 100°
B
【解析】连接AC，
∵AE、AF分别是BC、CD的垂直平分线，
∴AB=AC=AD，
∵AF⊥DC，AE⊥BC，
∴∠CAF=∠DAF，∠CAE=∠BAE．
∴∠DAB=2∠EAF=160°，
∴∠ABD=（180°-160°）÷2=10°，
∴∠ABC=∠ACB=30°+10°=40°；
在四边形AECF中，
∠FCE=360°-9... 如图所示的四个图形中，从几何图形变换的角度考虑，哪一个与其他三个不同?请指出这个图形，并简述你的理由．
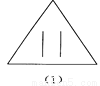
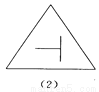
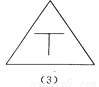
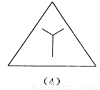
图(2)，仅它不是轴对称图形
【解析】试题分析：观察图形发现（1）（3）（4）都是轴对称图形，而（2）不是轴对称图形，由此即可得出结论．
试题解析：【解析】
（1）（3）（4）都是轴对称图形，而（2）不是轴对称图形．故从几何图形变换的角度考虑，图（2）与其它三个不同． 解方程：
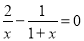
x＝－2
【解析】试题分析：按照解分式方程的步骤解方程即可.
试题解析：去分母，得
去括号，得
移项，得
合并同类项，得
检验：当时，
是原方程的解. －9a2b＋3ac2－6abc各项的公因式是_______；
－3a
【解析】根据提公因式法因式分解，可知其是首项为“﹣”的多项式，因此可知其公因式为-3a.
故答案为：-3a.