题目内容
在“线段、锐角、三角形、等边三角形”这四个图形中，其中是轴对称图形的有___个，其中对称轴最多的是__________.
3 等边三角形
【解析】线段有两条对称轴，锐角有一条对称轴，等边三角形有三条对称轴，
故答案为：3，等边三角形．
练习册系列答案
相关题目
如图,点D,E是正三角形ABC的边BC,AC上的点,且CD=AE,AD,BE相交于点P,BQ⊥AD于点Q,已知BE=7,则AD等于( )
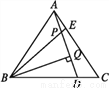
A. 5 B. 6 C. 7 D. 8
C
【解析】【解析】
∵△ABC是等边三角形，∴AB=AC，∠BAC=∠C=60°．
又∵AE=CD，∴△ABE≌△CAD（SAS），∴AD=BE=7．
故选C． 若a－b＜0，则下列各式中一定正确的是（ ）
A、a＞b B、ab＞0 C、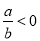
D、－a＞－b
D
【解析】
试题分析：由a－b＜0可得a＜b，再根据不等式的基本性质依次分析各项即可.
a－b＜0，
∴a＜b，
∴－a＞－b，但无法确定ab与的符号，
故选D. 如图，∠AOB＝30°，角内有一点P，PO＝10cm，两边上各有一点Q，R(均不同于点O)，则△PQR的周长的最小值是多少？
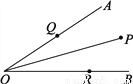
10cm
【解析】试题分析：设点P关于OA的对称点是E，关于OB的对称点是F，当点R、Q在EF上时，△PQR的周长=PQ+QR+PR=EF，此时周长最小．
试题解析：作出点P关于OA的对称点E，作出点P关于OB的对称点F，连接EF，交OA于Q，交OB于R．连接PQ，PR，PE，PF，OE，OF，
则PQ=EQ，PR=RF，
则△PQR的周长=PQ+QR+PR=EQ+QR+R... 如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=______。
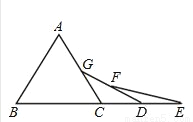
15°
【解析】试题分析：设∠E=x，根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
【解析】
设∠E=x，
∵DF=DE，
∴∠DFE=∠E=x，
∴∠CDG=∠E+∠DFE=2x，
∵CG=CD，
∴∠CDG=∠CGD=2x，
∴∠ACB=∠CDG+∠CGD=2x+2x=4x，
∵∠ACB=70°，... 如图，已知△ABC中，AC+BC=24，AO，BO分别是角平分线，且MN∥BA，分别交AC于N，BC于M，则△CMN的周长为（ ）
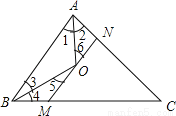
A.12 B.24 C.36 D.不确定
B
【解析】
试题分析：由AO，BO分别是角平分线求得∠1=∠2，∠3=∠4，利用平行线性质求得，∠1=∠6，∠3=∠5，利用等量代换求得∠2=∠6，∠4=∠5，即可解题．
【解析】
由AO，BO分别是角平分线得∠1=∠2，∠3=∠4，
又∵MN∥BA，∴∠1=∠6，∠3=∠5，
∴∠2=∠6，∠4=∠5，
∴AN=NO，BM=OM．
∵AC+BC=24... 老师拿出6根小木棒，3根长的相同，3根短的也相同，且长的是短的的长度的2倍，请用这6根木棒摆成四个完全相同的三角形．
见解析
【解析】试题分析：用3根长的构成一个大等边三角形，3根短的构成一个小等边三角形即可．
试题解析：【解析】
如图． 分式方程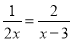
的解是_____．
x=﹣1
【解析】试题分析：根据解分式方程的方法可以求得分式方程的解，记住最后要进行检验，本题得以解决．
【解析】
方程两边同乘以2x（x﹣3），得
x﹣3=4x
解得，x=﹣1，
检验：当x=﹣1时，2x（x﹣3）≠0，
故原分式方程的解是x=﹣1，
故答案为：x=﹣1． 把多项式－x2＋x提取公因式－x后，余下的部分是( )
A. x B. x－1 C. x＋1 D. x2
B
【解析】根据因式分解的提公因式，提取公因式-x，可得－x2＋x=-x（x-1），所以剩余部分为x-1.
故选：B.