题目内容
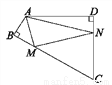
如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC、CD上分别找一个点M、N，使△AMN周长最小时，∠AMN＋∠ANM的度数为( )
A. 130° B. 120°
C. 110° D. 100°
B
【解析】作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值，作DA延长线AH，
∵∠DAB=120°，
∴∠HAA′=60°，
∴∠AA′M+∠A″=∠HAA′=60°，
∵∠MA′A=∠MAA′，∠NAD=∠A″，
且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，
∴∠AMN...
练习册系列答案
学习实践园地系列答案
相关题目
当x=-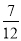
时,式子(x-2)2-2(2-2x)-(1+x)·(1-x)的值等于( )
A. -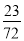
B.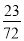 
C. 1 D.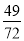 
A
【解析】【解析】
原式====．故选A． 如图，在等腰三角形ABC中，∠ABC=90°，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F，若AE=4，FC=3，求EF长．
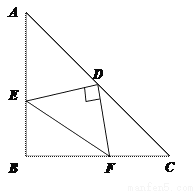
连结BD，证△BED≌△CFD和△AED≌△BFD，得BF=4，BE=3，再运用勾股定理求得EF=5 如图，AD是△ABC的角平分线，DE⊥AB于E，DF⊥AC于F，直线AD交EF于点O.问直线AD是线段EF的垂直平分线吗？请说明理由．
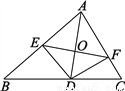
AD是线段EF的垂直平分线，理由见解析
【解析】试题分析：由AD为△ABC的角平分线，得到DE=DF，推出∠AEF和∠AFE相等，得到AE=AF，即可推出结论.
试题解析：∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE=DF，∠AED=∠AFD=90°，
∴∠DEF=∠DFE，
∴∠AEF=∠AFE，
∴AE=AF，
∴点A、D都在EF的垂直... 等腰三角形一腰上的中线将它的周长分别为8和12两部分，则它的腰长、底边长分别为__________________.
8,8,4或
【解析】设底边长a,腰长b,则有
（1）a+=8，
b+=12，
解得：a=4，b=8，
即腰长、底边长分别为：8，8，4；
（2）a+=12，
b+=8，
得a= ，b=，
即腰长、底边长分别为： ， ， ，
综上，腰长、底边长分别为：8，8，4或， ， ，
故答案为：8，8，4或， ， . 请充分发挥你的想象力，任选其一完成下面的设计
（1）以一直角三角形为“基本图形”，利用旋转而得到一个风车或风轮图案．你能设计出几种风车风轮图案呢？请将你的图案画出来，完成后与同学进行交流．
（2）利用圆、三角形、正六边形，通过平移或旋转来设计一个图案，完成后与同学交流你的作品，说明你的设计意图．
见解析
【解析】试题分析：根据旋转的角度不同可得到不同的风车形状，只要满足题意即可．
试题解析：【解析】
选（1），所画的是旋转90°的情况． 将点A绕另一个点O旋转一周，点A在旋转过程中所经过的路线是_______.
圆
【解析】
试题分析：根据圆的定义，到定点的距离等于定长的点的轨迹是圆．
依题意，点A绕点O旋转一周的路线是圆． 若关于x的方程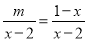
有增根，则m的值为( )
A. 0 B. 1 C. －1 D. 2
C
【解析】试题解析：方程两边同乘以x?2，得
①
∵原方程有增根，
∴x?2=0，
即x=2.
把x=2代入①，得
m=?1.
故选C. 多项式15m3n2+5m2n﹣20m2n3的公因式是（ ）
A. 5mn B. 5m2n2 C. 5m2n D. 5mn2
C
【解析】多项式15n²+5m²n?20m² 中，
各项系数的最大公约数是5，
各项都含有的相同字母是m、n，字母m的指数最低是2，字母n的指数最低是1，
所以它的公因式是5m²n.
故选C.