题目内容
等腰三角形一腰上的中线将它的周长分别为8和12两部分，则它的腰长、底边长分别为__________________.
8,8,4或
【解析】设底边长a,腰长b,则有
（1）a+=8，
b+=12，
解得：a=4，b=8，
即腰长、底边长分别为：8，8，4；
（2）a+=12，
b+=8，
得a= ，b=，
即腰长、底边长分别为： ， ， ，
综上，腰长、底边长分别为：8，8，4或， ， ，
故答案为：8，8，4或， ， .
练习册系列答案
相关题目
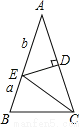
如图，在△ABC中，AB=AC，∠BAC = 36°，DE是线段AC的垂直平分线，若BE=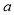
，AE=
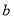，则用含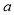、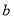的代数式表示△ABC的周长为 ．
2a+3b
【解析】
试题分析：由题意可知：AC=AB=a+b，由于DE是线段AC的垂直平分线，∠BAC=36°，所以易证AE=CE=BC=b，从可知△ABC的周长△ABC的周长为：AB+AC+BC=2a+3b.
故答案为：2a+3b． 如果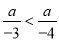
，则a必须满足（ ）
A、a≠0 B、a＜0 C、a＞0 D、a为任意数
C
【解析】
试题分析：根据不等式的基本性质即可判断.
，
∴a＞0，
故选C. 如图，直线AB∥ CD，∠ B=50°，∠ C=40°，则∠E等于（ ）
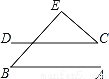
A. 70° B. 80° C. 90° D. 100°
C
【解析】试题分析：根据平行线的性质得到∠1=∠B=50°，由三角形的内角和定理可得∠E=180°﹣∠B﹣∠1=90°，故答案选C． 如图，在△ABC中，AB=AD=DC，∠BAD=26°.求∠B和∠C的度数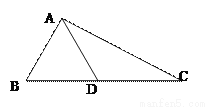
77° 38.5°
【解析】【解析】
∵ AB＝AD，
∴∠B＝∠ADB． ……………… 2分
∵在△ABD中，∠B+∠ADB+∠BAD＝180°，∠BAD＝26°，
∴∠B＝∠ADB＝77°． ……………… 4分
∵AD.＝DC，
∴∠DAC ＝∠C． ……………… 6分
∵∠ADB＝∠DAC+∠C， ……………… 7分
∴∠ADB＝2∠C，
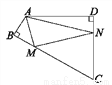
... 如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC、CD上分别找一个点M、N，使△AMN周长最小时，∠AMN＋∠ANM的度数为( )
A. 130° B. 120°
C. 110° D. 100°
B
【解析】作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值，作DA延长线AH，
∵∠DAB=120°，
∴∠HAA′=60°，
∴∠AA′M+∠A″=∠HAA′=60°，
∵∠MA′A=∠MAA′，∠NAD=∠A″，
且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，
∴∠AMN... 你能用一张长方形的纸片折出一个正三角形吗？动手试一试，简单叙述你的折法．
如图，先把矩形纸片对折，然后在沿着BM对折使C落在EF上的N点，再折出BM和CN即可．
【解析】试题分析：把长方形纸片ABCD的宽对折，然后展开，折痕记为EF，再把AD边折起，点D折叠到EF上，与EF的重合点为M，在CD上的折痕为点G，再沿GM对折，在AB上的折痕为H，则三角形AHG就是一个正三角形．
试题解析：【解析】
如图，
连接AM，在△AMG和△AMH中，
AM=... 解方程：
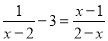
x＝3
【解析】试题分析：按照解分式方程的步骤解方程即可.
试题解析：去分母，得
去括号，得
移项，得
合并同类项，得
系数化为1，得
检验：当时，
是原方程的解. 4x(m－n)＋8y(n－m)2中各项的公因式是________.
4(m－n)
【解析】根据题意，先变形为4x(m－n)＋8y(m－n)2，把m-n看做一个整体，即可找到公因式4（m-n）.
故答案为：4（m-n）.