若m＜n，比较下列各式的大小：
（1）m－3______n－3 （2）－5m______－5n （3）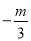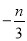
______
（4）3－m______2－n (5)0_____m－n （6）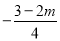
_____
< > > > > <
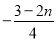
【解析】(1)m用“＞”或“＜”填空：
（1）如果x－2＜3，那么x______5； （2）如果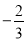
x＜－1，那么x______
；
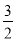（3）如果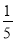
x＞－2，那么x______－10；（4）如果－x＞1，那么x______－1．
< > > <
【解析】(1)如果x-2<3,那么x<5;
(2)如果,那么;
(3)如果,那么x>-10;
(4)如果-x>1,那么x<-1. x＜y得到ax＞ay的条件应是____________．
a＜0
【解析】∵x＜y得到ax＞ay是两边同时乘以a，不等号的方向发生了改变，∴a＜0． 若x＋y＞x－y，y－x＞y，那么
（1）x＋y＞0，（2）y－x＜0，（3）xy≤0，（4）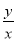
＜0中，
正确结论的序号为________.
（2）
【解析】
试题分析：由x＋y＞x－y，y－x＞y，可得x＜0，y＜0，再根据不等式的基本性质即可得到结果。
∵x＋y＞x－y，y－x＞y，
∴x＜0，y＜0，
∴x＋y＜0，y－x＜0，xy＞0，＞0，
则正确结论的序号为（2）. 满足－2x＞－12的非负整数有________________________．
0，1，2，3，4，5
【解析】∵不等式-2x＞-12的解为x＜6，∴满足x＜6的非负整数有0，1，2，3，4，5． 若ax＞b，ac2＜0，则x________．
＜
【解析】由ac2＜0，结合c2为正可知a＜0，
对ax＞b两边同时除以a，得x＜ .故答案为：＜. 如果x－7＜－5，则x__________；如果－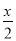
＞0，那么x_________．
＜2 ＜0
【解析】根据不等式的基本性质1，不等式x?70两边同时乘以?2,不等号的方向改变,则如果?>0，那么x<0.
故答案为：<2；<0. 当x 时，代数式2x－3的值是正数.
＞
【解析】
试题分析：先由题意列出不等式，再根据不等式的基本性质即可得到结果。
由题意得2x－3＞0，解得x＞. 根据不等式的基本性质，把下列不等式化成“x＞a”或“x＜a”的形式：
（1）4x＞3x+5 （2）－2x<17
（3）0.3x＜－0.9 （4）x＜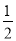
x－4
（1）x＞5；（2）x＞；（3）x＜－3．（4）x＜－8
【解析】分析：（1）直接利用不等式的基本性质1对不等式进行变形即可；（2）利用不等式的基本性质3对不等式变形即可，注意不等号的方向；
（3）利用不等式的基本性质2对不等式变形即可；
（4）先利用不等式的基本性质1对不等式进行变形，再利用不等式的基本性质2对不等式变形即可.
本题解析：
（1）4x＞3x+5
... 若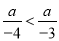
，试判断a的正负性．
a为负数
【解析】分析：先根据不等式基本性质3,两边都乘以,再根据不等式基本性质1,两边都减去3a即可得出结论.
本题解析：根据不等式基本性质3，两边都乘以－12，得3a＞4a．
根据不等式基本性质1，两边都减去3a，得0＞a ，即a<0 ，即a为负数．