题目内容
x＜y得到ax＞ay的条件应是____________．
a＜0
【解析】∵x＜y得到ax＞ay是两边同时乘以a，不等号的方向发生了改变，∴a＜0．
练习册系列答案
相关题目
求满足下列条件的∠A的度数（精确到1″）：
（1）cosA=0.8607；
（2）tanA=56.78．
（1）30°36′18″；（2）88°59′28″
【解析】试题分析：（1）熟练应用计算器，使用2nd键，然后按cos-1 0.8607，即可求出∠A的度数，对计算器给出的结果，用四舍五入法取近似数．
（2）方法同（1）．
试题解析：
解：（1）∵cosA=0.8607，
∴∠A≈30.605°=30°36′18″；
（2）∵tanA=56.78，
∴∠A... 如图,如果AB∥DE,那么∠BCD=( )
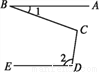
A. ∠2=∠1 B. ∠1+∠2 C. 180°+∠1-∠2 D. 180°+∠2-2∠1
C
【解析】试题分析：过点C作CF∥AB，
∴∠1＝∠BCF，
∵AB∥DE，
∴DE∥CF，
∴∠DCF＝180°－∠2，
∴∠BCD＝∠BCF＋∠DCF＝∠1＋180°－∠2＝180°＋∠1－∠2．
故选：C． 下列不等式中，不含有x＝－1这个解的是
A. 2x＋1≤－3 B. 2x－1≥－3
C. －2x＋1≥3 D. －2x－1≤3
A
【解析】A. ∵ 2x＋1≤－3 ，∴x≤-2，∴不含有x＝－1这个解;
B. ∵ 2x－1≥－3，∴x≥-1，∴含有x＝－1这个解
C. ∵－2x＋1≥3 ，∴x≤-1，∴含有x＝－1这个解
D. ∵－2x－1≤3，∴x≥-2，∴含有x＝－1这个解
故选A. 当x 时，代数式2x－3的值是正数.
＞
【解析】
试题分析：先由题意列出不等式，再根据不等式的基本性质即可得到结果。
由题意得2x－3＞0，解得x＞. 已知有理数a、b、c在数轴上的位置如图所示，则下列式子正确的是（ ）
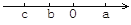
A. cb＞ab B. ac＞ab C. cb＜ab D. c＋b＞a＋b
A
【解析】试题分析：先根据数轴的特点得出a＞0＞b＞c，再根据不等式的性质进行判断：
A、∵a＞0＞b＞c，∴cb＞0＞ab. 选项正确.
B、∵c＜b，a＞0，∴ac＜ab. 选项错误.
C、∵c＜a，b＜0，∴cb＞ab. 选项错误.
D、∵c＜a，∴c+b＜a+b. 选项错误.
故选A． 如图，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13.求四边形ABCD的面积．
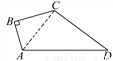
36.
【解析】试题分析：连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．
试题解析：【解析】
连接AC．如图所示：
∵∠B=90°，∴△ABC为直角三角形．又∵AB=3，BC=4，∴根... 如图，在等边三角形ABC中，∠B、∠C的平分线相交于点O，作BO、CO的垂直平分线分别交BC于点E、F.小明说：“E、F是BC的三等分点．”你同意他的说法吗？请说明理由．
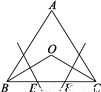
同意，理由见解析
【解析】试题分析：连接OE、OF，根据等边三角形角平分线的性质，可得∠OBC=∠OCB=30°，由BC的垂直平分线，可知BE=OE，∠EBO=∠EOB=30°，∠OEF=60°，再证，∠OFE=60°，得出△OEF为等边三角形，从而可知EF=OE=BE=OF=FC，得出结论．
试题解析：同意．理由如下：
连接OE、OF，
∵E为BO垂直平分线上的点，且∠O... 解分式方程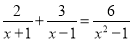
，分以下四步，其中，错误的一步是( )
A. 方程两边分式的最简公分母是（x–1）（x+1）
B. 方程两边都乘以（x–1）（x+1），得整式方程2（x–1）+3（x+1）=6
C. 解这个整式方程，得x=1
D. 原方程的解为x=1
D
【解析】试题分析：方程无解，虽然化简求得，但是将代入原方程中，可发现和的分母都为零，即无意义，所以，即方程无解